微分方程式をコンピュータで解く手法の一つにルンゲクッタ法というものがある。理工系学生は、C言語などのプログラミングの授業で習う。こう言うと敷居が高いように感じるかもしれないが、一般的な表計算ソフトのExcelでも簡単にできるんだ!ということを言いたくて、書くことにした。一度、Excelで手軽にルンゲクッタ法によって数式が解ける!ということがわければ、特に精度を求めない限り、自分で作った方程式を記述して、解くことができる。是非、自由に作って、どんどん色んな現象を予測してみてほしい!
そもそもルンゲクッタ法って何なの?何ができるの?
学者やエンジニアは、現象を解析し、予測するために、数式化を行う。この数式を、微分方程式という。微分方程式は、「時間tの変化に対する注目している量Xの変化量が、どういった要素に依存するか?」という視点で記述される。そして、解くというのは、「X=〇t・・・」や「X=近似値」で表すことをいう。後者を数値計算という。この数値計算の、精度がよく、一般的な手法が、ルンゲクッタ法である。アルゴリズムは下記である。
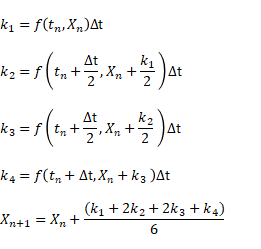
どうやって使うのか?
ルンゲクッタ法は、数式の近似解を求める手法である。関数式の近似というと、理系学生ならテーラー展開がピン!と来るであろう。それを利用した物である。詳細は、関係書籍やWikiなどを見て勉強してほしい。使い方は下記である。

まず、解析対象の現象を微分方程式の形で記述する。次に、一階方程式の形に変換する。微分方程式にはd^2X/dt^2 といった二階の形で記述される項が出てくることがある。このままだと計算できないので、それをdY/dtなどの形に変換しなおす。( 後に示す例題で理解を深めてください。)
ここまで来たら、初期値を設定します。開始時間、その時間の変数の値、時間刻みなどを決める。そして、ルンゲクッタ法をコンピュータに記述します。例えば、Excelに記載すると、下図のようになる。

最後に、上図の黒太線で囲った領域を一ブロックとしてコピーし、必要な精度が得られるまで、下のセルにコピーを繰り返す。
[参考書籍:林卓郎(2009), 振動系のダイナミクス, オーム社 ]
具体例
例えば、下記のような数式を上記の手法で解いてみる。
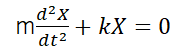
求めたいのは、ある時間でのXの値である。しかし、このままでは二階の微分方程式なので、一階化をする。
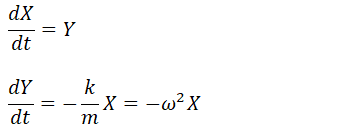
これで、一階の微分方程式になった。二階のものは、一階の項を別の変数でまとめ、その変数を使って二階を一階で示せばいいわけである。言葉で書くと混乱するが、上式を見てもらえれば容易に分かると思われる。
次に、初期値の設定をする。上式は高校や大学の物理でよく登場する振動系の式である。簡単のために、M=k=1, Xo=1, Yo=0, to=0, Δt=0.5 とする。
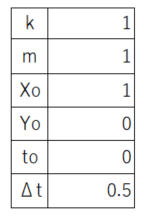
では、これをルンゲクッタ法でExcelに記述してみることにする。
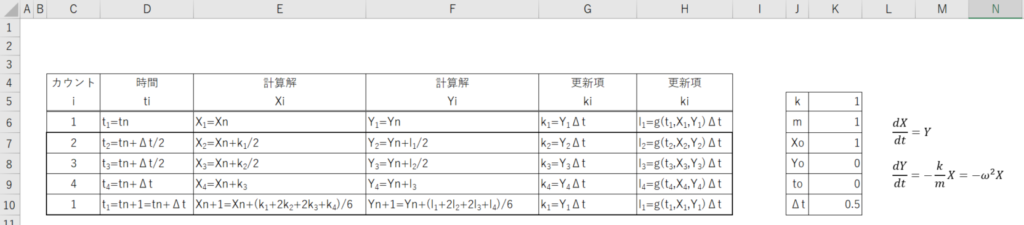
※ 画像が小さい方は、画像上にマウスのカーソルをあわせ、右クリックし、「画像だけを表示」 をクリックすると大きく見られます。
分かりやすくするために、上図のように、公式を記述した。速度成分である、Y(=dX/dt)も横に書いてみた。更新項のkは、Xに対する物。同lは、Yに対する物である。 では、実際に公式の下に記述することにする。
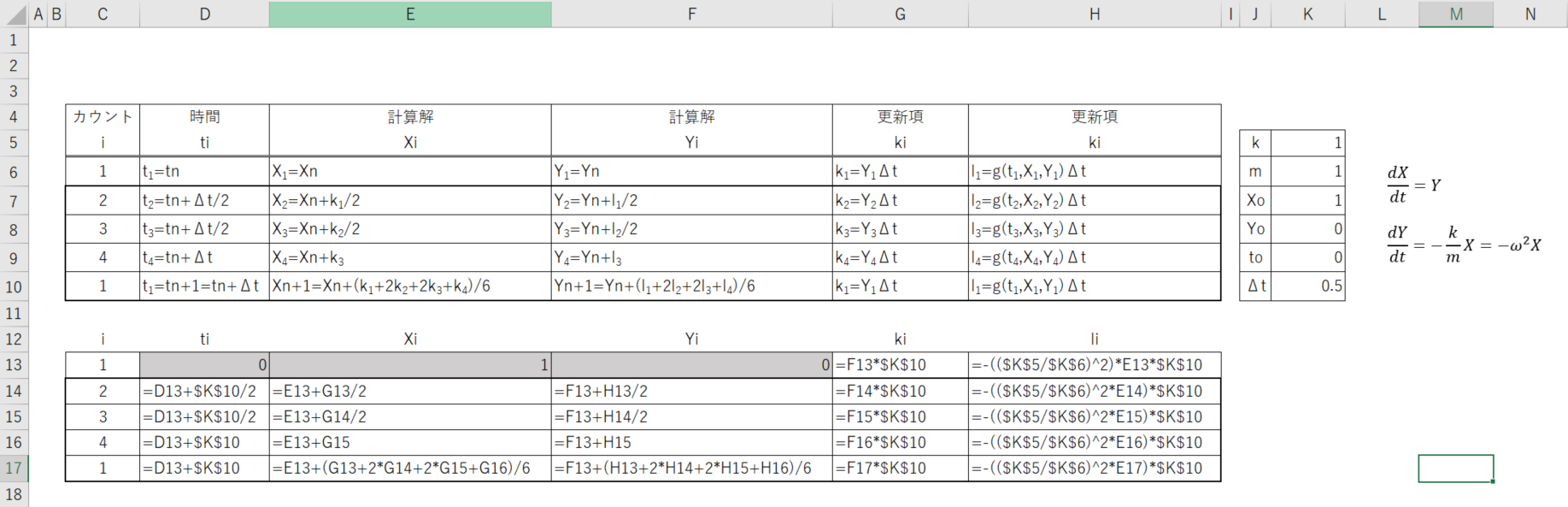
上図の黒網部は、初期値である。わざと記入した数式を文字列で示している。数式に戻すと…
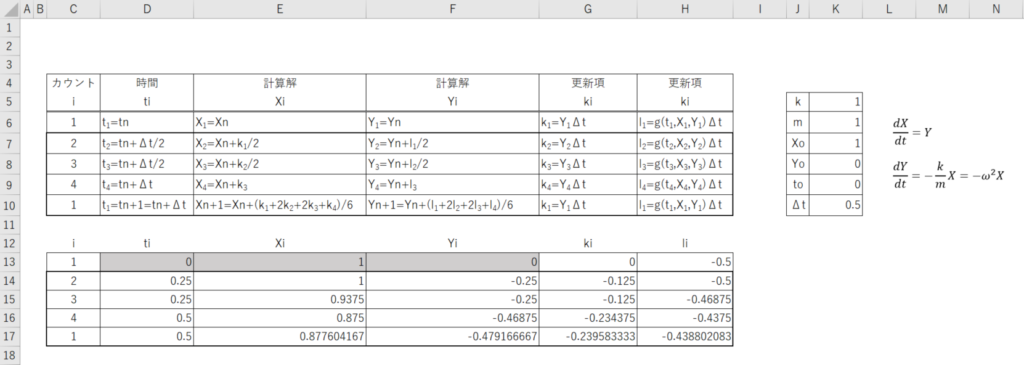
となる。ここで、先ほどの順序に従って、2~1をコピーして、下のセルに貼り付けていく。
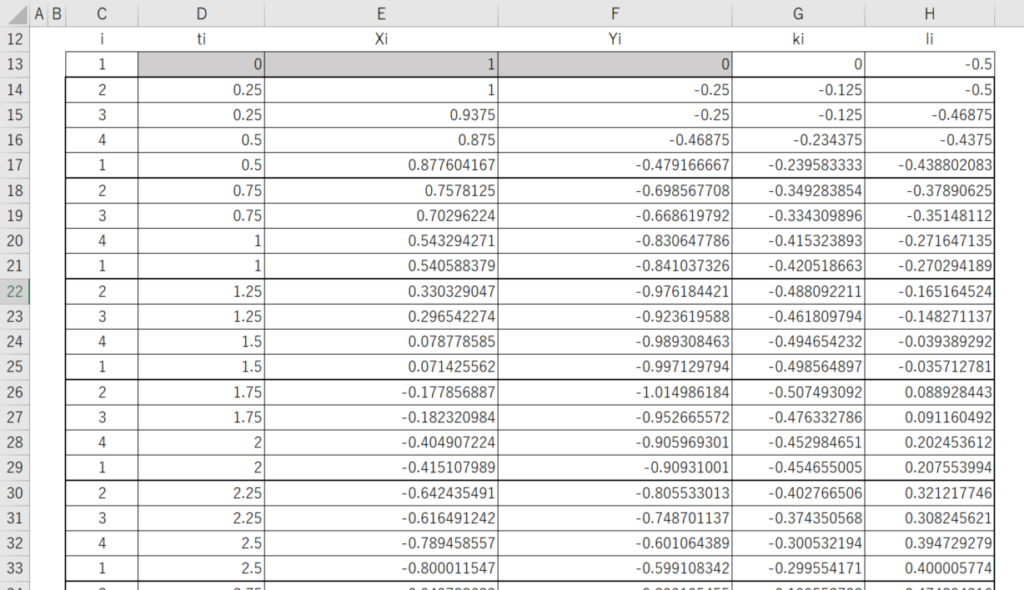
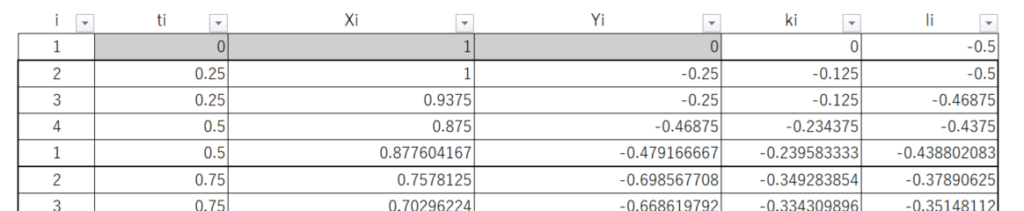
ここで、i=1の奴のみ表示させてグラフ化すると、Xの時間変化を見ることができる。i=1のみ表示させる方法だが、上図のi~liの部分をドラックして、「並べ替えとフィルター」を押し、ジョウロのようなマークをクリックすれば、表上のチェックボックスを表示させられる。そこのiの部分をクリックし、1を選択してみると、1のみの値だけに絞った表ができあがる。

項目をドラッグする。

赤丸箇所をクリック。

フィルターを押す。
グラフ上にチェックボックス( 小さな▼付きの吹き出し )ができる。
上図 i の部分をクリックし、1 だけにチェックを入れる。
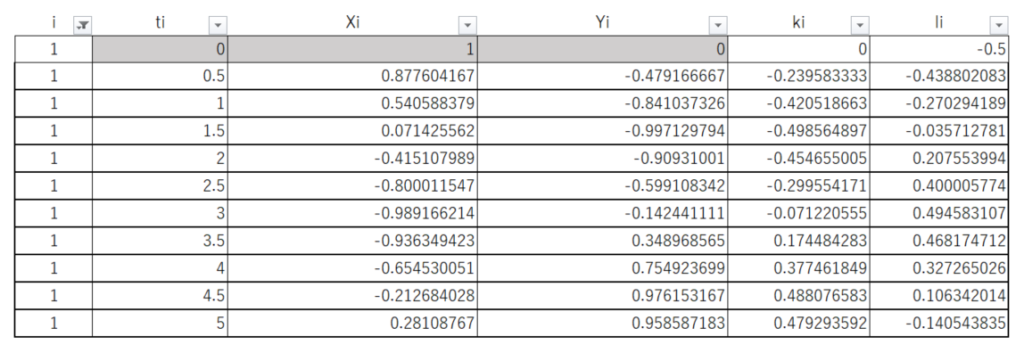
試しに、0≦t≦5までのXをグラフ化してみる。
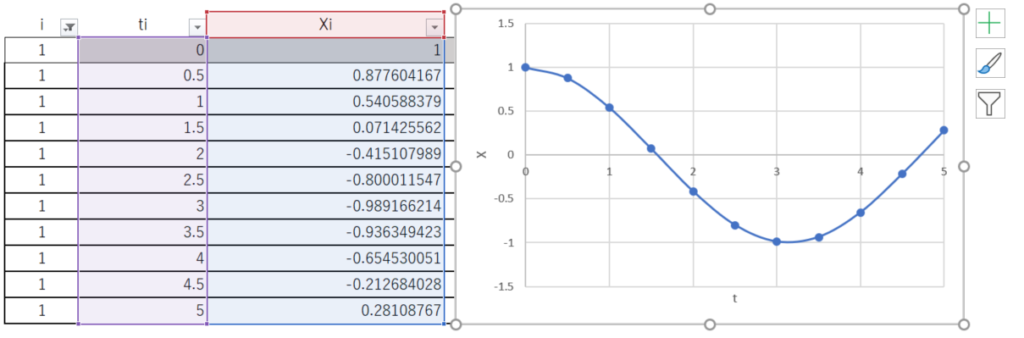
このように、ルンゲクッタ法により解くことができた。振動している様子がよくわかる。非線形方程式も基本的に同じやり方でやることができる。数式をセルに記述するのは面倒だが、是非、試してみてほしい。
(参考) Excel計算フォーマットを作る際の注意
(参考)連立微分方程式をRK法でExcelで解く方法
こんにちは
ルンゲクッタ法自体理解できない状態なのですが、連立微分方程式をグラフ化したくて辿り着きました。
>後藤 さま
管理人です。コメントありがとうございます。連立微分方程式をルンゲクッタ法でExcelで解く方法を本日記事にするので、そちらをご確認下さい。また、連立微分方程式の解のグラフ化については、Excelだと「時間-着目変数」と「着目変数1-着目変数2」にして考察するのが一番手っ取り早いと思います。というのも、Excelでは「着目変数1-着目変数2-着目変数3」を容易に良い感じで3D表示することが難しいので、いたずらに時間を浪費するからです。では、よろしくお願いします。