立ち食いそば屋の儲けのからくり

出張先で、急いでいるときなど、立ち食いそば屋に駆け込むことがある。そんなとき、「かけそば」を頼んだりする。我ながら、しみったれているな～と思いつつ、麺をすすり、急いで店を出るわけである。そんなとき、数秒間決まって思うのが、「立ち食いそば屋さんってなんで儲けているのだろうか？」ということである。今日は、色々調べて分かったことを述べたいと思う。

立ち食いそば屋さんって？

日本の鉄道を使ったことがある人は、駅構内やホームにそば屋さんがあるのを見たことがあると思う。あれが、「立ち食いそば屋」さんである。

安く、早く、手っ取り早く美味しいお蕎麦を食べられるので、懐の寂しい庶民には、ありがたい食事処である。

最大の魅力は、安さであろう。かけそば一杯で250円ほどである。

質素倹約な生活をしている私は、学生時代から週に一度は、この立ち食いそば屋さんにご厄介になっていました。笑

原価はどのくらいなのか？

とある書籍によると、「麺30円＋ダシ汁20円＋ネギ10円＝60円」が、かけそば一杯の材料費である。これに、人件費と光熱費が加算されると、、、かけそば一杯の原価は、250円ほどになる。

つまり、かけそば客ばかりがいくら来ても、全く利益が出ないのである。

何で儲けているのか？

サイドメニューである。おにぎり、唐揚げ、かき揚げ、サラダなどが、大体あると思う。大体、100円の値がついていると思われる。

おにぎりは、輸入米や、古米を安く仕入れて、一合も米を炊けば、🍙が二個作れる。一個当たりの原価は、約20円である。よって、100円の🍙を買ってくれれば、80円ほどの利益がでるのである。唐揚げ、かき揚げやサラダに使う野菜などは、輸入野菜を使って安くすませば10～20円ほどで作れるので、売れれば🍙と同じくらい儲けられる。

立ち食いそば屋さんに行って、かつ、お腹と懐に余裕があったら、サイドメニューを頼んであげましょう。自分のお腹、お店も豊かになるので、小さなWIN-WINを体験できると思う。

まとめ

・立ち食いそば屋さんは、かけそばでは売り上げがでない。

・サイドメニューが売れてこそ、利益がでる。

・お客さんが、サイドメニューを頼みたくなる工夫をしよう。

お店の野菜に注意しよう

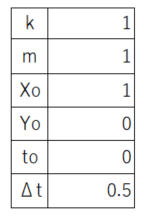
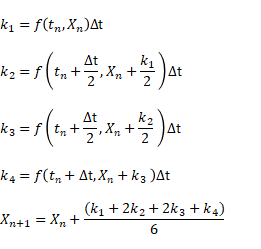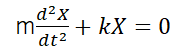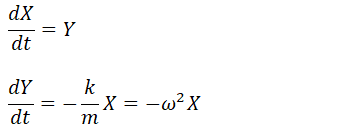私の会社では、社員食堂がある。管理栄養士さんが栄養バランスを考えて作った定食が、一食300円で振舞われる。大変ありがたい話である。しかし、昔から思っていたのは、ドレッシングやタレのついていない箇所で感じる、野菜やお肉の味は、とても不味いということである。日本の食堂に出される野菜やお肉は安全なはずだ！と思っていたが、この価格の安さと明らかにスーパーで買う野菜と異なる味に疑問を感じ、本当に安全なのか？を調べることにした。

日本にはどのくらいの野菜が輸入されているのか？

2012年の統計データによると、日本の食料自給率は生産額ベースで68％。残り32%が輸入品です。この内の15%が、輸入野菜です。よって、輸入野菜は、全体でみれば、生産額ベースで4.8%が出回っているわけです。

輸入野菜は何処で消費されているのか？

スーパーや八百屋さんでは、あまり見かけません。これらの多くは、外食産業、中食産業、加工食品に使われています。

※1 外食産業：家庭外での食事を提供する産業。ex) レストラン
※2 中食産業：家庭と外食産業以外の食事を提供する産業 ex) 惣菜屋、弁当屋

なぜ使われるのか？

これらの輸入野菜が、外中食産業で使われる理由は、以下と考える。

・国産と比べて3～6割ほどの安価だから

・残留農薬量の管理に対して、外国産は国内の信用を得ていないから

・これらの業界では、産地表示が義務つけられていないから。

同じキャベツでも、価格が国産の3割ともなれば、味や見ためさえ整えれば、1/3の価格で作れるのは自明である。または、国産で真面目に作った物と同額で売れれば、原価率を大幅に下げられるので、笑いが止まらいのは当然である。後者のような在り方は、消費者からすればたまったものではないが、産地表示や検査基準が不透明なのだから、やりたい放題である。

※3 検査基準：輸入時の検査は、書類検査で9割ほどが完了し、実際の検査は1割弱

輸入野菜の危険性

輸入野菜には、残留農薬が大量に含まれている可能性があるものの、検査が甘いので、容易に市場に出回っていることは述べました。それ以外に問題なのは、ポストハーベストです。これは、収穫後の管理と輸送の時に必要な、防カビ剤、殺菌剤、防虫剤のことです。いわゆる、食品添加物に分類されます。

これらは、国産野菜では、発がん性の危険があることから使用制限がかけられています。しかし、外国産は、そうではないのです。農薬よりも、場合によっては毒性が強く、残留している可能性が高いので、特に注意が必要なのです。こうした物が、レストラン、お弁当、お惣菜、レトルト食品、加工品に大量に使われているという事実を知らなけれなりません。話題の、スムージーなどは、大いに危険です。野菜の栄養素は、加工時の熱と圧力で破壊され、農薬や添加物が濃縮されて残るのですから…。こうした物を買って、常飲している方々、、、あなたのDNAは確実に変性させらていると思います。ご注意を。。。

まとめ

・安い食堂(社食など)の料理は、輸入材料を使って賄っているから安いのである。

・輸入野菜は、残留農薬と食品添加物が大量に含まれている可能性がある。

・これら添加物は、発がん性の疑うがあるので国産では禁止されているほど危険である。

・外食、お弁当、レトルト食品、食品加工物(スムージー)は極力減らそう。自分で育てて、作ろう。

Excelによるルンゲクッタ法の使い方

微分方程式をコンピュータで解く手法の一つにルンゲクッタ法というものがある。理工系学生は、C言語などのプログラミングの授業で習う。こう言うと敷居が高いように感じるかもしれないが、一般的な表計算ソフトのExcelでも簡単にできるんだ！ということを言いたくて、書くことにした。一度、Excelで手軽にルンゲクッタ法によって数式が解ける！ということがわければ、特に精度を求めない限り、自分で作った方程式を記述して、解くことができる。是非、自由に作って、どんどん色んな現象を予測してみてほしい！

そもそもルンゲクッタ法って何なの？何ができるの？

学者やエンジニアは、現象を解析し、予測するために、数式化を行う。この数式を、微分方程式という。微分方程式は、「時間tの変化に対する注目している量Xの変化量が、どういった要素に依存するか？」という視点で記述される。そして、解くというのは、「X＝〇t・・・」や「X＝近似値」で表すことをいう。後者を数値計算という。この数値計算の、精度がよく、一般的な手法が、ルンゲクッタ法である。アルゴリズムは下記である。

どうやって使うのか？

ルンゲクッタ法は、数式の近似解を求める手法である。関数式の近似というと、理系学生ならテーラー展開がピン！と来るであろう。それを利用した物である。詳細は、関係書籍やWikiなどを見て勉強してほしい。使い方は下記である。

まず、解析対象の現象を微分方程式の形で記述する。次に、一階方程式の形に変換する。微分方程式にはd^2X/dt^2 といった二階の形で記述される項が出てくることがある。このままだと計算できないので、それをdY/dtなどの形に変換しなおす。( 後に示す例題で理解を深めてください。)

ここまで来たら、初期値を設定します。開始時間、その時間の変数の値、時間刻みなどを決める。そして、ルンゲクッタ法をコンピュータに記述します。例えば、Excelに記載すると、下図のようになる。

最後に、上図の黒太線で囲った領域を一ブロックとしてコピーし、必要な精度が得られるまで、下のセルにコピーを繰り返す。

[参考書籍：林卓郎(2009), 振動系のダイナミクス, オーム社 ]

具体例

例えば、下記のような数式を上記の手法で解いてみる。

求めたいのは、ある時間でのXの値である。しかし、このままでは二階の微分方程式なので、一階化をする。

これで、一階の微分方程式になった。二階のものは、一階の項を別の変数でまとめ、その変数を使って二階を一階で示せばいいわけである。言葉で書くと混乱するが、上式を見てもらえれば容易に分かると思われる。

次に、初期値の設定をする。上式は高校や大学の物理でよく登場する振動系の式である。簡単のために、M=k=1, Xo=1, Yo=0, to=0, Δt=0.5 とする。

では、これをルンゲクッタ法でExcelに記述してみることにする。

※ 画像が小さい方は、画像上にマウスのカーソルをあわせ、右クリックし、「画像だけを表示」をクリックすると大きく見られます。

分かりやすくするために、上図のように、公式を記述した。速度成分である、Y(=dX/dt)も横に書いてみた。更新項のｋは、Xに対する物。同ｌは、Yに対する物である。では、実際に公式の下に記述することにする。

上図の黒網部は、初期値である。わざと記入した数式を文字列で示している。数式に戻すと…

となる。ここで、先ほどの順序に従って、2～1をコピーして、下のセルに貼り付けていく。

ここで、i=1の奴のみ表示させてグラフ化すると、Xの時間変化を見ることができる。i=1のみ表示させる方法だが、上図のi～liの部分をドラックして、「並べ替えとフィルター」を押し、ジョウロのようなマークをクリックすれば、表上のチェックボックスを表示させられる。そこのiの部分をクリックし、1を選択してみると、1のみの値だけに絞った表ができあがる。