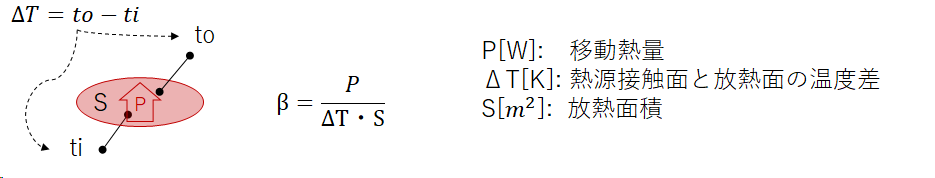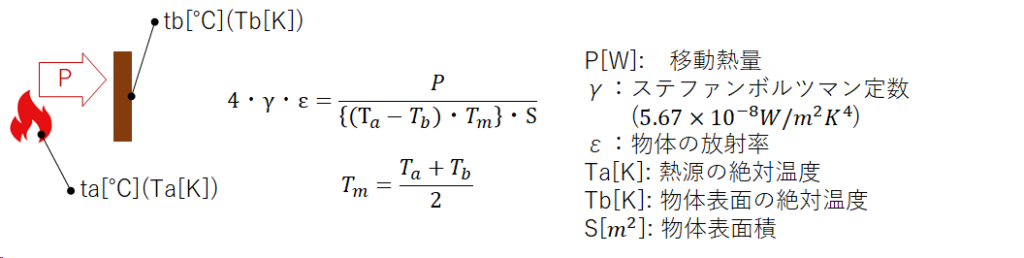勉強するとき、創造するときに言ってはならない言葉がある。それは「難しい」である。
難しいという言葉は、何か困難にぶち当たったときに口にする。
しかし、勉強しているときや、物を作るときに、それは言ってはならない。
なぜなら、「難しい」と口にすることを一つの答えにしてしまい、分析や前進が止まってしまうからである。また、難しさを理解したところで有益なことは何もない。むしろ、恐怖心をもってしまい、何度学習しても身につかなくなる。以下、数学問題、議論、物作りにおいて、「難しい」と言いそうになった場合の、私の試みをあげる。
数学の問題と考えてみる。
まず、最終的に問われている「〇〇を求めよ」を知る。ここで、難しいと分かったところで、何も得られることはない。ゴールが分かったら、そこに向かうために何が必要か分析をするのである。分析とは、必要と思われる要素を書き出し、一つ一つ点検する作業である。樹形図をイメージするとよい。
要素の書き出しは、如何に多くの問題に触れたかが鍵となる。よって、何かの試験に臨むものは、多くの問題に触れ、「引き出し」を沢山身に着けることが肝要である。
また、処理能力を高めるために、「計算力」と「判断力」を養うこと大事である。
計算力とは、四則演算、微分積分、因数分解、そろばん、暗算etc
判断力とは、「〇か✖かを、ある基準で判定すること」である。ある基準は、自分で定める。この能力は、自分で何かを決める意識や癖を持つだけで日々養える。
これらは、筋トレと同じく、やればやっただけ身につく。
二つ目の例として、「議論」をあげる。これは、議題に対して、意見を言い合い、二項対立を探す。そして、それについて意見を言い合い、感情的でなく客観的な判断を積み重ねて、結論を導く。
この時、AとBという対立意見があったときに、Aの主張者が、Bの主張者にその欠点を指摘されて「難しい」と言ってしまったら、どうなるであろうか?それは、Aという主張は、Bの主張者の突っ込みへの解がないことを意味する。
議論なれしている者ならば、その欠点を保留にしつつ、すかさずBの主張の欠点も述べ、欠点の多少、欠点の質を列挙しあう方向に誘導し、直近の問題に対して数と質のどれで対応するかを判断するように議論を導くであろう。こうしなければ、Aの主張は消えてしまうからである。
最後に、エンジニアとして物を作るときのことをあげる。設計という仕事は、楽しい反面、孤独で責任の重い仕事である。特に機構設計の仕事は、回路設計、ソフト設計に比べて、要求事項も、時間もお金も莫大にかかり、社会的責任の重さも比較にならないほど重たい仕事である。
開発の上流下流の不具合、社会情勢、販売戦略に伴う急な設計変更など日常茶飯事である。「難しい」議題しかないのである。こうしたとき、難しいと言っているだけでは、何も生まれない。まずは、冷静に、その場でできることを列挙するのである。ネットで調べてもよい、書籍から引っ張てきてもよい、開発メンバーでもよい、とにかく出来る方法をあげるのである。
このとき、よくコストや日程が成り立ってないなら、✖ と頭ごなしに言う人がいるが、そんな意見は、たとえ上司でも真に受けてはいけない。コストや日程が成り立つ方法が思いつくなら、とっくに提示しているからである。それがその時間で導いた答え(限界)なのである。
✖といって、日程をくれるのなら再考する。くれないなら、お金と日程を犠牲にしてでもやるしかない。製品において、品質悪が最もよくないことだからである。
以上、「難しい」という言葉の無意味さと、問題・議論・物作りの現場でそう言いたくなる状況を仮想し、私がどのように日常立ち向かっているかを述べた。参考にするとともに、何かアドバイスがあれば、連絡いただきたい。
まとめ
・学びと創造の場では、「難しい」という言葉は、無意味である。
・難しいと言いたくなったら、なぜ難しいのか考え、書き出しましょう。
・書き出した項目について、考えられる解を考えましょう。