よくサスペンス系の映画やドラマを見ていると、被害者の死亡推定時刻を予測するシーンがある。あれってどうやるのかな?とフト思い、予測してみることにした。
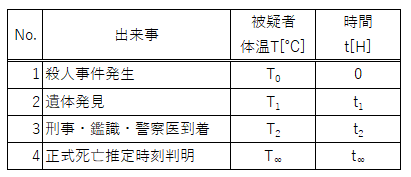
まず、サスペンスドラマでの死亡推定時刻は〇〇と表現されるまでの大まかな出来事を整理してみる。
状況整理
殺人事件発生 → 遺体発見 → 刑事、鑑識、警察医到着 → 暫くして正式推定時刻判明
次に、この出来事に対する、体温と時刻の関係を考えてみる。この関係を定性的に考えてみて、モデル化しようという腹である。
事件発生直後は、被疑者の体温は、生きているときと同じである。後は、生命活動が失われているので、外気温に向かって下がる一方である。したがって、
T0>T1>T2 という関係が成り立つ。
ここで、体温の減衰の仕方をイメージしてみる。温度は、高温から低温に向かって下がる。その下がり方は、その温度差による。したがって、温度差が大きいときは急速に下がっていくが、温度差が小さくなるとその下がり方は緩やかになる。
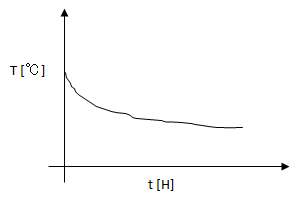
こんな感じ…
このことから、指数関数的に減衰していくモデルと考えてよいのではないかと思う。
数式化
指数関数的なモデルとすると、体温の時間変化はその時の体温に依存すると考える。
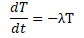
これを変数分離して、t=0 で T=To とすると、解は、
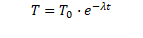
となる。今、わかっていないのは、λ である。これは定数で、今回の場合、体温の減少する速度を左右する量である。固有値という人もいるが、この場合、減衰する前提であり、発散などは考えていないからこの概念を出さないほうが、感覚的に分かりやすいと思う。
λが分かれば、上式のtに、警察医たちが到着したときの被害者の体温T2、そのときの時間t2を代入して、t2について式を整理すれば、死亡推定時刻が判明する。
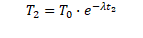
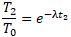
両辺に対数をとって、t2について整理すると、、、
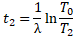
となる。この値を、警察医が現場に到着した時刻から引けば、殺人事件の起こった時間が分かるのである。
では、λはどうやれば求まるであろうか?
なんのことはない。t2からある時間経過後に、もう一度体温を測定して、どれだけ体温が下がったかを明らかにすればよい。
仮に、ある時間t∞のときの体温をT∞とする。
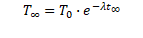
(3)式/(6)式より、Toを削除して式を整理する。
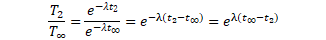
・・・(7)
Δt = t∞ – t2 として、(7)式の最両辺に対数をとり、λについて整理する。
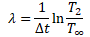
こうしてλが求まる。後は、(8)式を(5)式に代入すれば、t2が求まり、それをその時の時刻から引くことで、死亡推定時刻(=殺害時刻)が求まる。
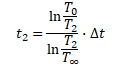
以上で、簡単だが、モデル化ができた。では、Excelで数値を記入して見たいと思う。

仮に、上記の入力項のように数値を定めてみる。出力項のλは(8)式、t2は(9)式である。どうやら、警察医が来る約5時間前に事件が発生したと予測できるのである。。。※ 上記の値は、実測に即したものではない。
この考えだと、もし犯人が、死亡推定時刻の算出を狂わそうするのならば、殺害時の体温を高くしたり、低くしたりするカラクリをしこんでおけばよいことになる。
昔、「名探偵コ○ン」で、エアコンを入れといて云々というカラクリがあったが、そういうことである。ただし、警察は優秀なので、そうした隠蔽のカラクリは必ず気が付きます。
サスペンス小説を書こうとしている方は、この辺だと読者をあ!っと言わせにくいので、別の「点と線」を考えたほうが良いと思います。
では!