日本では、高校生の頃から理科の授業で、電気に関する現象を扱う。クーロンの法則、ガウスの法則、コンデンサー、フレミングの法則(左/右)、電気回路、電子回路などは、頭を悩ませた記憶があるのではないだろうか?私は、高校時代に何度も赤点を取りました。笑 しかし、一念発起し、一つ一つ丁寧に学んでいくことで、気が付けば最も得意な科目になっておりました。本ブログでは、今後、定期的に基礎電気磁気学と基礎電気回路、電子回路を紹介していきたいと思います。
電気って何?
電気とは、電荷[C]の動きによって起こる現象のことです。例えば、おもむろに金属製のドアノブに触れたときにバチッとなることがあると思います。あれは、体内に溜まっていた電荷が、金属のドアノブが近づき、そこに移動することでおこる現象です。このとき、バチッと感じたり、ビリッと感じたり、感じ方に大小があると思います。これを感覚的に表現していたら現象を客観的に捉えられないがないので、定量的に表現できるように定義した量が、電荷です。
学問的な体系は?
電気の存在は、古代より知られていました。例えば、よく教科書に書かれているのは、琥珀をこすると鳥の羽毛が引き寄せられる現象です。古代ギリシャの記録文の中に登場したりしています。
日本では、江戸時代に平賀源内が壊れたオランダ製の静電気発生装置(エレキテル)を修復して使えるようにし、人々を驚かしたという記述があります。
電気現象が学問として躍進したのは、18世紀に入ってからです。まず、クーロン(仏)が電荷間に働く力の関係性を見つけました(クーロンの法則)。その後、ガウス(独)が、面に拡張して電界(電場)として整理しました(ガウスの法則)。
この時、電気と似た現象である磁界も、学問の基本的な視点である「等価性」から電界に対比させる形で定義と整理をされてきました。その際、磁荷、磁気クーロンの法則、ガウスの法則の磁界バージョンであるビオサバールの法則が作られました。
今までお話ししたことは、全て静止した電荷や磁荷と、その周囲に作られる力の強さ(=電界、磁界)、位置エネルギー(=電位、ポテンシャル)の話です。また、電界や磁界は互いに似ていると分かっていても、どのように関係しているのかは分かりませんでした。そんなときに登場したのが、アンペール(仏)です。彼は、配線に電流を流すと、その周囲においた方位磁針が動く という現象を発見し、その定式化に成功しました(アンペールの法則 )。電流は、電荷の時間変化です。つまり、電荷の変化と磁界の関係を整理することに成功したわけです。いわば、動電界の記述の成功です。
この後、ファラデー(英)が、レンツ-ファラデーの電磁誘導の法則を発表します。これは、コイルに磁石を出し入れして磁界の大きさを変えてやると、流れる電流値が変わるというものです。数式としては、磁束の変化に対して電位が変わるという形で整理されております。こうして、動磁界の記述に成功しました。
19世紀に入り、マクスウェル(英)が光や電磁波の研究の中で、光は電磁波であることをファラデーまでの理論で記述することに成功しました。これが、有名なマクスウェルの方程式です。大学で物理を専攻すると、必ず電気磁気学の講座があります。このとき、全体像を理解させて細部の理論を教えてくださる先生方は、まず、マクスウェルの方程式を黒板に書きます。しかし、私の経験上さっぱり分からなかったので、ここでは、数式を語る前に、背景を長々と述べることにしました。
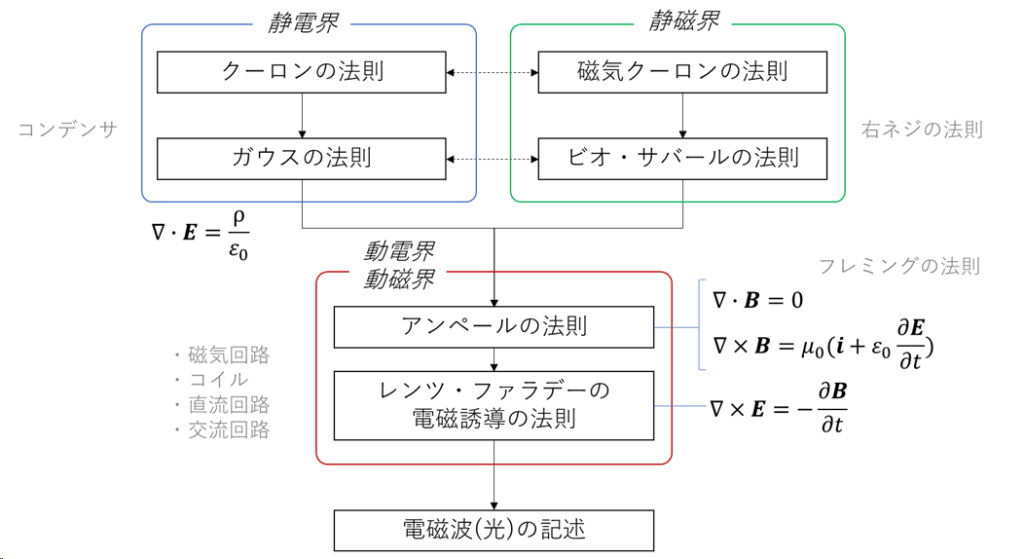
以上を、一つの図にまとめると下記のようになります。
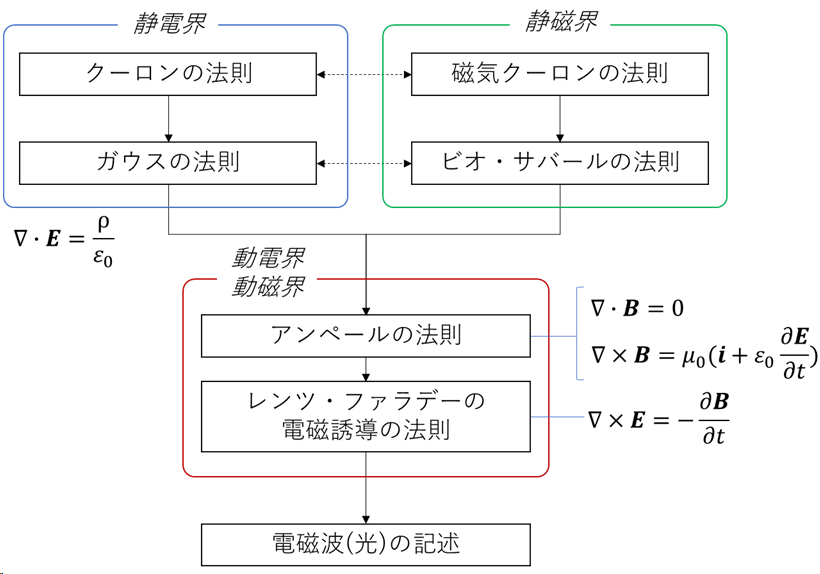
電気回路は、この電気磁気学をベースにして、より工学的に使いやすい形に整理したものです。コンデンサの問題は静電界ですし、U字磁石の間に電気の流れた配線を通した時に配線にかかる力は、静磁界から動電界、動磁界までの間の成果で記述されます。電気回路の問題を解いていて、なんでこうするのか分からない!!??となったら、電気磁気学の教科書を紐解くとスッと分かることがあると思いますよ。
まとめ
・電気とは、電荷の動きによる現象の一つです。
・学問的には、電気磁気学で基本的な理論が語られます。
・電気磁気学から、電気回路理論、電子回路理論が発展していきます。
高校生の方は、下図の高校教科書に載っている公式を正しく暗記しましょう。そして、回路理論の学習をしてください。
大学生の方は、下図を心に描きながら電気磁気学を履修し、マクスウェル方程式に整理されるまでを理解して、電気回路や電子回路、電気電子材料などを学んでください。授業の際は、いつも心に下図を描き、迷子にならないようにしてください。途中、電位、ポテンシャル、電気数学、電束、磁束、磁気双極子etc といった用語が出てきますが、下図の何処なのか追記しながら学習すると迷子になりにくいです。