日頃の業務の中で、大量のデータがない中で判断しなければならないことはないだろうか？

こうしたときに役に立つのが、ベイズ統計である。

主観的確率統計などと言われることがある。条件付き確率という形で、高校の頃に習った人もいるかもしれない。

どうやって使うのか？

ベイズ統計では、まず、統計的に判断したい現象について、物語を作るところから始まる。物語は、「このように判断するかどうかを、こういう現象が起こるかどうかで決めよう。起きたら、判断は正しかったとより思えるし、起きなかったら別の判断をするべきだったと思う。」という感覚で作る。

もう少し具体的に書くと、「Aと判断したら、XまたはYという現象が起こりうる。Bと判断しても、XまたはYという現象が起こりうる。」という具合にする。

そして、AやBと判断する確率、および、AまたはB毎のXとYの起こりうる確率を、経験や議論で定める。ここで、起こりうる全てのパターンが自然に出来上がるので確率P[%]を求めておく。

次に、XまたはYという結果から、AやBと判断する確率を修正する。この箇所が、ベイズ統計による判断である。主観的と言われる所以は、起こりうる物語毎の確率を仮置きして求めるからだと私は思っている。

ベイズ統計の優れたところは、仮置きで一応の判断ができることと、それを少ない実験で精度を訂正していけるところにある。

こうした理論上の性質から、ベイズ統計は、企業が重要な判断を、コストや倫理的な犠牲を払わずに行うのに適している。では、具体的にどのように仮定し、更新していくのか、一例をあげたいと思う。

具体的にやってみる。

問題：合コンで初見の人が、信頼できる人かどうかを判断したい。

例えば、「相手が信頼できるかどうかを、会話の中で、正直者か嘘つきかで見極めよう。」と考える。

先のAとB、XとYに当てはめてみる。

A：信頼できる。

B：信頼できない。

X：正直なことをいう。(= 嘘をつかない )

Y：嘘つき。

Aと判断したら、XまたはYという現象が起こりうる。Bと判断しても、XまたはYという現象が起こりうる。

ここまでできたら、下のような樹形図を作って、起こりうるストーリーの確率を求める(まだ、実際には起こっていない)。

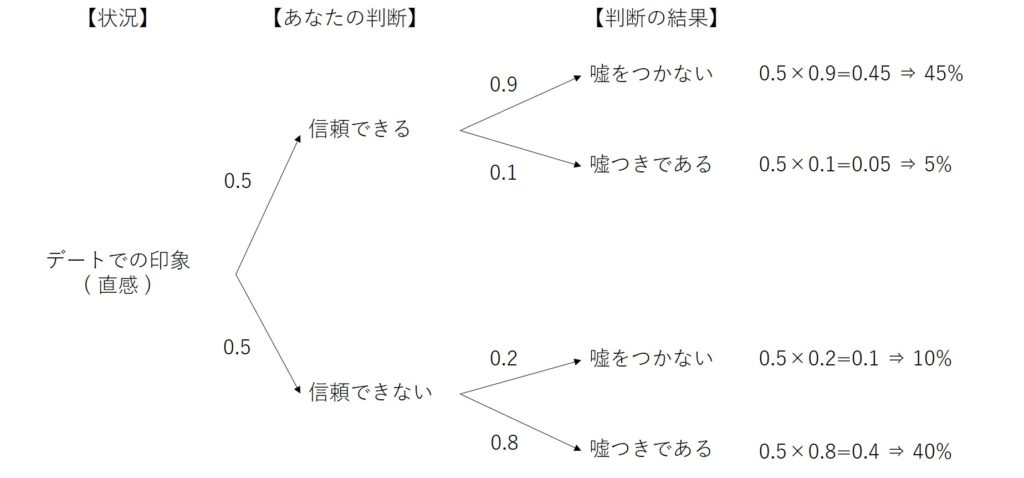
初回デートで、相手の雰囲気からその人が信頼できる確率を、偏見なしの50％とする。そして、その場合、嘘をつかない確率を90%、嘘をつく確率を10％とおく。すると、最終的なストーリーの発生確率は上図のようになる。同様に、信頼できない場合の嘘つくつかない確率も仮定し、最終的なストーリーの発生確率を求める。

この分岐毎の確率は、自己の経験や専門家(占い師)などの意見をきくなりして決めると、精度がより上がる。

マトリクスにまとめると下図のようになる。

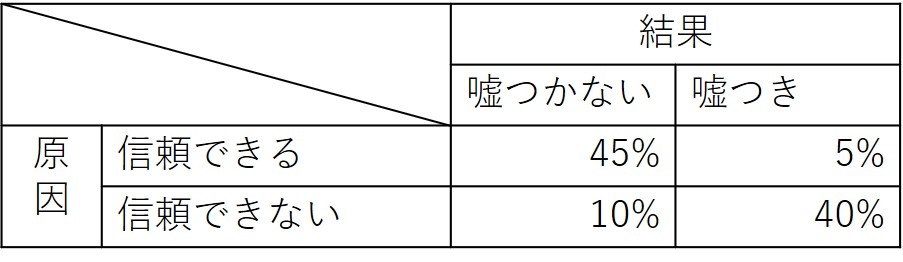
これが初回デート前のシミュレーションである。この条件下で、デートに臨み、相手が、もし自分に対して嘘をついたとする。すると、その嘘により、信頼できる確率が下図のように修正されることになる。

デートの前は、初見での信頼できる確率を偏見なしに50%としていたのだが、一回目のデートで相手が嘘をついたので、それは11%に下がってしまった。逆に、信頼できない確率は89%まで上昇した。これを元に、二回目のデートをするかどうかを判断するのはあなた次第である。図にすると下記のようになる。

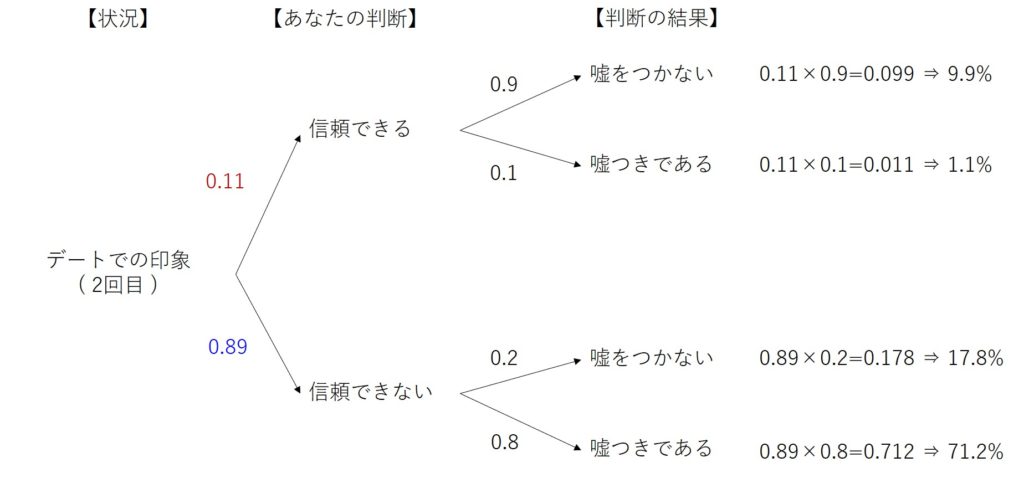
「信頼できて、嘘つかない」と願うあなたの思いは、9.9%しかないと判断できる。また、4つの起こりうる確率から、この人は、「信頼できず、嘘つき」である確率が最も高く、付き合うに値しない人であると判断できる。

このように、未知の減少で、お金や時間、倫理的理由など限られた条件下で、何らかの根拠をもって重要な判断しなければならないときに、ベイズ統計は有効である。

是非、仕事で、使ってみてほしい。この考え方は、経験をもとに判断し、経験によって修正するという我々人間の特性に近く、意外にすんなり受け入れられると思われる。

では！