今日は、前回に続き、数式の遊びを紹介する。テーマは、熱設計である。
熱設計とは、「製品開発において、物を作る前の構想時点で、熱源が冷えるような機構を考えること」を言う。この概念を知らず、モノが出来てから、筐体に孔をあけたり、適当なヒートシンクを持ってきて取り付けたりでは、昨今の高発熱密度な製品や部品を冷やすことは不可能である。
一重に熱設計と言っても、やり方は、問題設定によって様々である。
Q1:筐体内に、発熱量P[W]の熱源がある。これを何か特別な機構で排熱する必要があるか?
Q2:Q1で排熱する必要がある場合、どれだけの流体を当てればよいか?
Q3:高発熱密度な部品がある。この熱をある領域まで広げたい。どうする?
Q4:ある熱源がある。風が一方向から吹いている。これを冷やすには、どれくらいの空間と風量、ヒートシンクがあればよいか?
などなどである。
本日は、Q4について、一つのアプローチ方法を紹介する。大学、大学院で研究活動をしたことのある方は、必ず、最適化問題を何らかの形で触れたと思う。
本日紹介するQ4へのアプローチを理解した上で、是非、この方程式を、特定の量に対して最適化する方法を考えてみて欲しい。。それはきっと、あなたが真のエンジニアや研究者になったときに、問題を解決する素晴らしい力の源になると思うからである。また、是非、私にもそれを教えて欲しい。
【問題Q4】
ある熱源がある。風が一方向から流れている。この時、熱源を冷却するには、どれくらいの空間とヒートシンクがあればよいか?ただし、熱源の熱は、ヒートシンクに全て移動できるとする。また、ヒートシンクのフィンの加工上の制約条件は、無視しても良い。
********************************************************************
まず、条件を整理、仮定してみる。
◎ 熱源 ⇒ 発熱量 P[W]、目標温度 Tt[℃]、周囲環境温度 Ta[℃]
◎ 風 ⇒ 風量 Q[m3/min]
◎ 空間サイズ ⇒ 流路サイズと考える。
・流路幅 W[mm]
・流路長 L[mm]
・流路高さ H[mm]
◎ ヒートシンクサイズ
・FIN幅 ω[mm]
・FIN間距離 δ[mm]
・FIN数 n[枚]
・FIN長 L*[mm]
・FIN高さ H*[mm]
次に、これらを図示してみる。問題は、情報の仮定と整理をし、図示することで、より理解が深まる。これが「数式遊び」の極意であると、私は思っている。
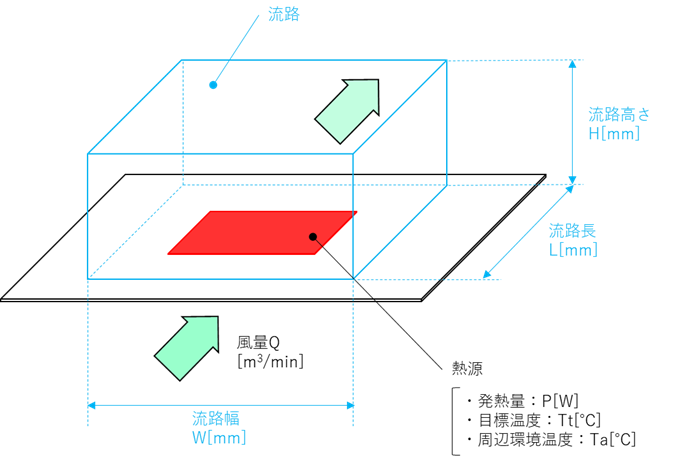
図1. 熱源と周辺空間(流路)の関係イメージ
ここで、問題で問われている、ヒートシンクについて考えてみる。ヒートシンクは、流路の中に位置する部品である。また、ヒートシンクは、流路に対して水平かつ短冊状にFINが配列される部品である。よって、例えば、下図のように仮定してあげれば良い。つまり、流路をヒートシンクのFINで刻んでやるのである。
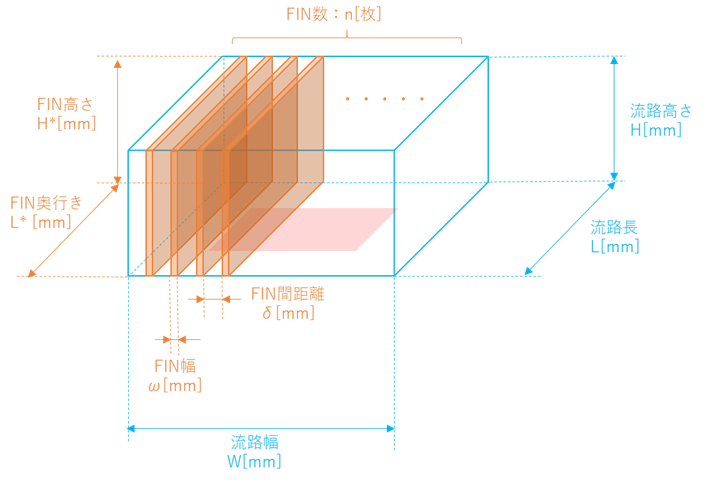
図2. 流路にヒートシンクを配置したイメージ
図2では、流路長L、流路高さHが、それぞれ、FIN奥行きL*、FIN高さH*と等しいとした。
さてこのように図化すると、例えば、以下のように、「熱源情報、寸法情報、風量」に関する関係式 を立式することができる。
1). ヒートシンクサイズに関する関係式
- 放熱面積:S = n × ( 2HL ) [mm2] ・・・①
- 包絡体積:V = WH = { nω + ( n+1 )δ }H [mm2] ・・・②
FIN数 n[枚], フィン高さH[mm], FIN奥行き(=流路長)L[mm]
ヒートシンク幅(=流路幅)W[mm], FIN幅 ω[mm], FIN間距離 δ[mm]
2). 熱伝達率hm[W/(m^2・K)]の定義式 と熱抵抗値R[K/W] の関係
- hm = P/{S・(Tt – Ta)} = P/(S・ΔT) [W/(m^2・K)] ・・・③
- R = (Tt – Ta)/P = ΔT/P [K/W] ・・・④
発熱量P[W], 目標温度Tt[℃], 周辺空気温度Ta[℃]
hm = 1/(S・R) [W/(m^2・K)] ・・・⑤
ここで、放熱面積Sの単位は、mm2 とすることが多いので、⑤式もそのようにしておくと便利である。つまり、
hm = 10^6/(S・R) [W/(m2・K)] ・・・⑤’
である。
なお、この式において、風が熱を空気中に移動させる能力である熱伝達率が分かっていれば、どれくらいの放熱面積が必要かが分かる。⑤’式を変形すると、、
S = 10^6/( hm・R ) [mm2] ・・・⑥
となる。少なくとも⑥式以上の放熱面積を取れば、よいと目算ができる。
- S ≧ 10^6/( hm・R ) [mm2]・・・⑦
3). 強制熱伝達率hmf [W/(m^2・K)] の関係式
- hmf = 3.86×(U/L)^0.5 [W/(m^2・K] ・・・⑧
- Q = AU [m^3/s] ・・・⑨
⑧式は、熱設計関係の書籍でよく登場する式である。論文などを見ると、条件別に色んな式があるので、適宜参照してほしい。。が、熱設計指針をざっくり立てるのが目的なら、、正直、この関係式だけ覚えておけば良い気もする。
⑨は、流体力学の初めの方に登場する、連続の式である。流路内において、流路断面積A[m2]と流速U[m/s]の積が一定というものである。⑧式に⑨式を代入すると、、、
- hmf = 3.86×{ Q/(AL) }^0.5 [W/(m^2・K)] ・・・⑩
風量 Q[m3/s], 流路断面積 A[m3], 流路長L[m]
となる。ここで、流路断面積Aは mm2で、風量Qは m3/min で考えることが多いので、これをQp[m3/min]として⑩式に代入する。
- hmf = 3.86×{ Qp/( 60AL )×10^8 }^0.5 [W/(m^2・K] ・・・⑩’
風量Qp[m3/min], 流路断面積A[mm2], 流路長L[mm]
以上の式から、⑦式と⑩’式を、hm = hmf とし、さらに⑦式に①式を代入すると、、「熱源情報、寸法情報、風量」に関する関係式 が導かれる。
S ≧ 10^6/[ 3.86×{10^8×Qp/(60AL) }^0.5 ]
↔
2nHLR ≧ 10^6/[ 3.86×{10^8×Q/(60AL) }^0.5 ]
式を整理すると…
- QL×(nHR)^2/A ≧ 6,350 ・・・⑪
となる。ここでさらに、流路断面積A = (n+1)δ×H なので、⑪式に代入して整理すると、、
- QHL×(nR)^2/{δ(n+1)} ≧ 6,350 ・・・⑫
となる。
後は、これに確定している量を代入して、欲しい未知量を求めれば良い。
例えば、良く開発現場で、この熱源を冷やすのに必要な空間とヒートシンクサイズを見積れと言われる。驚いたことに、使用できるFANが決まっていることもある。この場合、仮に、Q = 0.1m^3/min, R =1K/W とすると、、⑫式は、
HL×n^2/{δ(n+1)}≧63,500
を満たせば、何でも良いとなる。。さて、あなたは、これにどう答えるであろうか??変数は、4つである。如何にすれば、最適といえるであろうか??
定石は、変数の変域を定義するのである。。。が、開発現場では、これを否定されることの方が多い。理由は、(熱設計者が)変域を定義し、(承認者らが)それを許容して、最悪の条件が導かれたときに、(承認者らが)プライドが傷つくのを恐れてGoサインを出せないからと、かねがね感じている。話を戻して、変域を定義してみる。
例えば、
・1 ≦ H ≦ 30mm
・1 ≦ L ≦ 50mm
・1 ≦ W ≦50mm
・ω≧0.3mm
・δ ≧0.6mm
・n > 0
とする。Wは、ωn+δ(n+1)という具合にFINとの関係が深いので先にこちらを考える。W≦50mm より、、
0.3n+δ(n+1) ≦ 50mm
である。δ=0.6mmとすれば、0.3n+0.6n+0.6=0.9n+0.6≦50 なので、
n ≦ 54.8 ( ただし、δ = 0.6mm, ω = 0.3mm )
ここで、HとLの関係に式を詰めていく。
HL×54^2/{0.6(54+1)}≧63,500
↔ HL≧ 718 (1≦H≦30, 1≦L≦50)
このことから、最小のHとLは、HL=718の境界上の任意の数で良いので、、例えば、(H,L)=(14.36, 50) となる。
まとめると、熱抵抗値R=1K/W、風量Q=0.1m3/min の風が流れる流路において、フィン間距離δ=0.6mm、フィン幅ω=0.3mm、流路幅W=50mmとして、フィン数n=54枚 とすれば、、最小のフィン高さ(=流路高さ)H=14.36mm、最小のフィン奥行き(=流路長)=50mm と算出できる。。(あれ、あってんのか)。。色々課題を思いつきましたが、、、今日はここまでにしたいと思います。。
では。。
【本日の動画】相模川の水の煌めき
激しい流れに、太陽の光が反射し、キラキラ煌めいております。見ていると、雑念が払われて、スッキリしてきます。