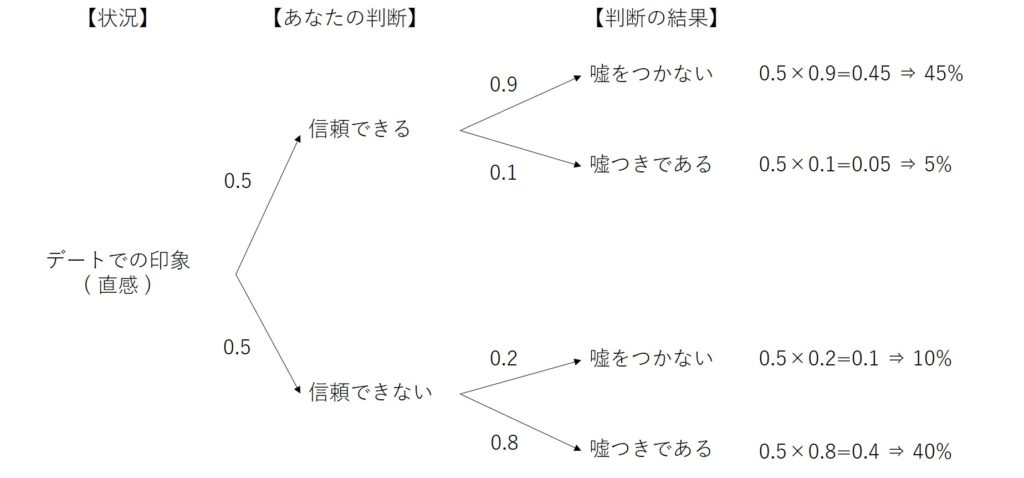
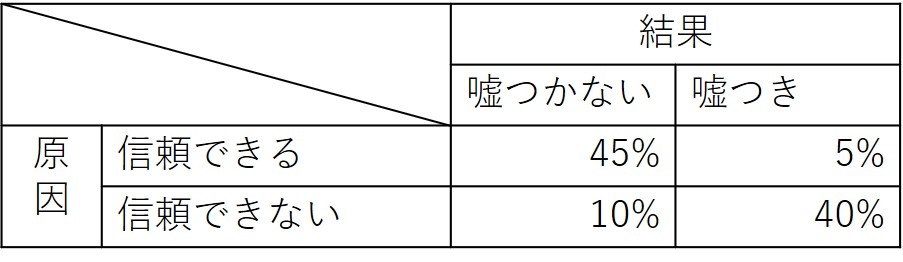
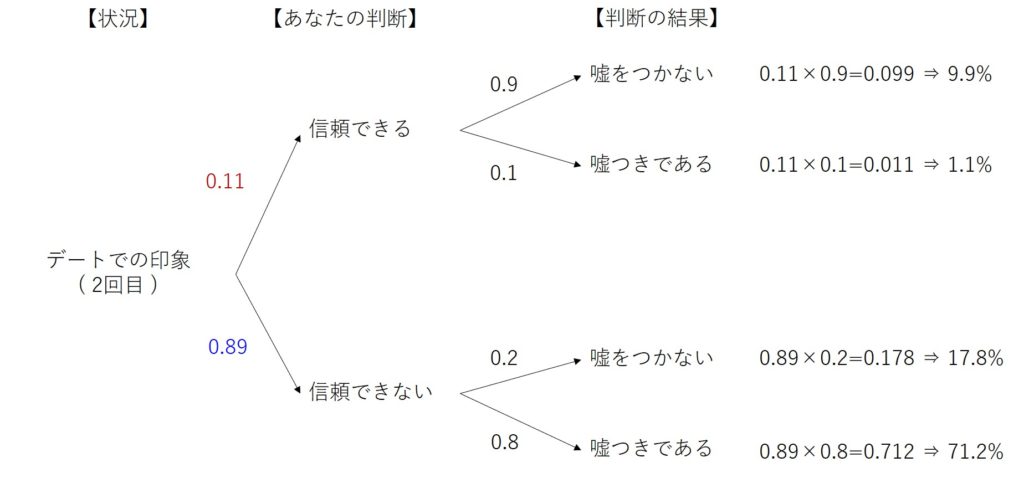
人類が古代から利用している道具に、滑車(pulley,block,tackle,sheave)という物がある。これは何であろうか?
滑車とは?
重い荷物をもち上げるのに使う道具である。 持ち上げようとする荷物を「少ない力で持ち上げたり」、 「加える力の方向を変えたり」 することができる。
先日、NHKの番組で、古代ローマのコロッセオの壮大な仕掛けについてのドキュメンタリーがやっていた。そこで、闘技場の地下に導いた猛獣(ライオン、象etc)をどうやって闘技場にあげたのか?という課題について再現実験がなされていた。
初めは、歯車とロープを使うモデルが提案されていた。男たちが力を合わせて歯車を回す。それによって檻の天面に結びつけられたロープが巻き上げられ、檻が上に上がるというものである。
しかし、檻の重さだけでも500kg程あり、とても上がらなかった。
そこで、現場担当のエンジニアが思いついたのは、滑車を使うということであった。
滑車の基本原理
滑車は、一般に、「定滑車」と「動滑車」がある。軸が天井などに固定されて動かないものを定滑車。軸に重りがぶら下がっており、滑車が動く物を動滑車という。
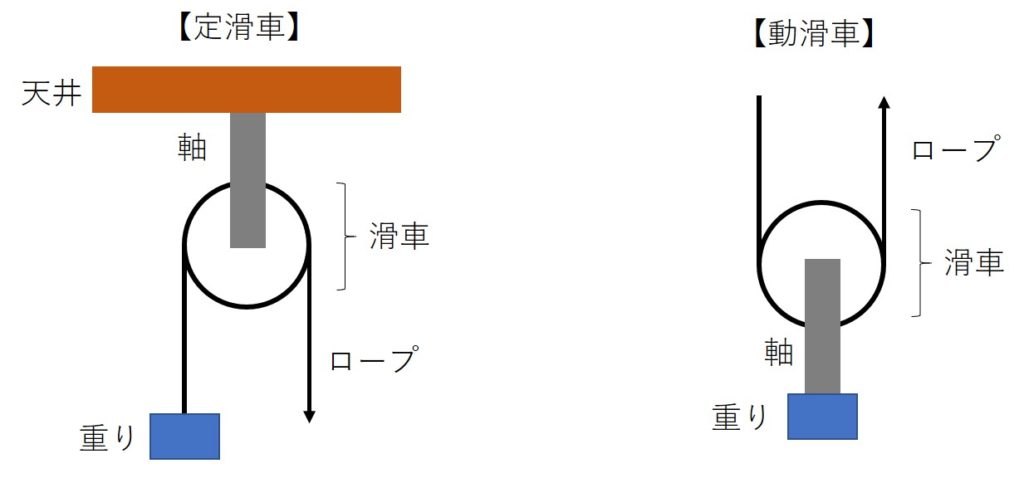
定滑車は、重りをもち上げるためには、重りと同じ力でロープを引っ張らなければならない。しかし、重りをもち上げるために、力を下に加えることでそれを実現できる。定滑車は、「重りと同じだけの力が必要だが、持ち上げるための力の向きを変換する効果」があるのである。
一方、動滑車は、重りに対して持ち上げる力の方向は同じだが、半分の力で持ち上げることができる。「持ち上げるための力の向きは同じだが、半分の力で持ち上げられる効果」がある。まとめると、下図のようになる。
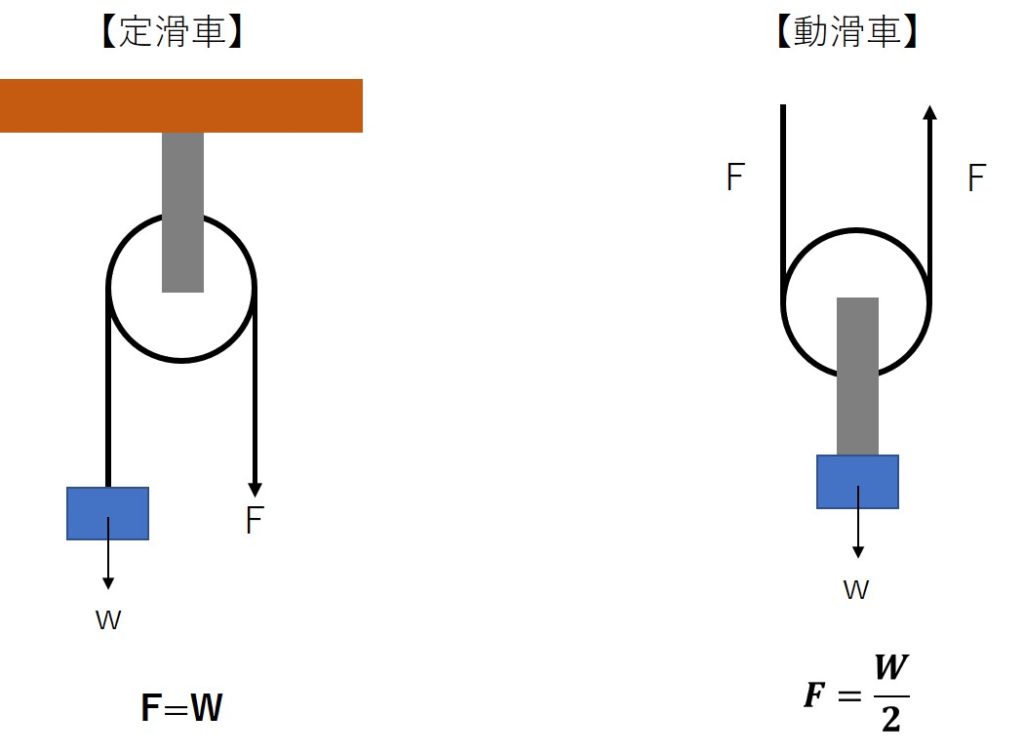
これらの性質から定滑車と動滑車を組み合わせることで、重りの重さに対して加える力をどんどん小さくすることができるのである。
(余談ですが、中学受験の理科のテストで、定滑車と動滑車を組み合わせた複合滑車の問題がしばしばでます。しかし、上の「二つの性質」と「力のつり合い」を知っていれば、全部解けます。)
滑車で重い物を軽い力で持ち上げる例
例えば、下記のような複合滑車を考えてみる。
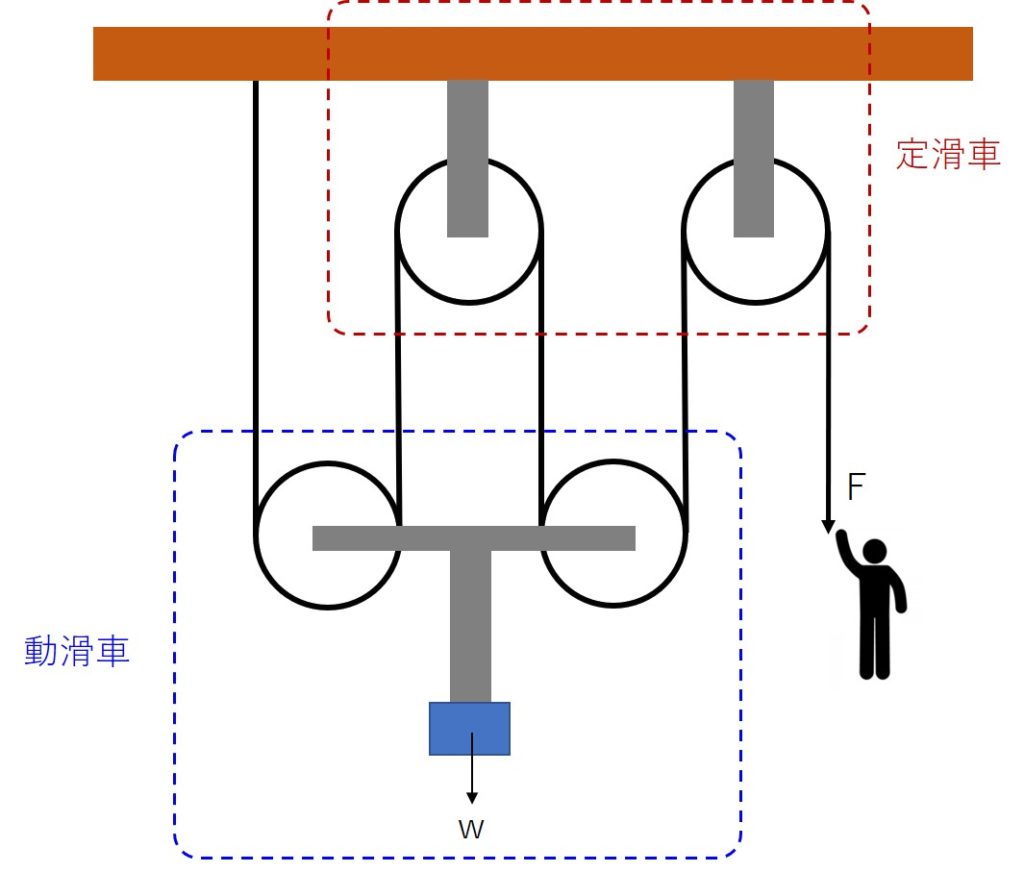
定滑車と動滑車が二つある。二つの動滑車は互いに軸で連結されており、連結部材の中央に、W[kg]の重りがぶら下がっている。滑車の重さは無視するとする。FとWの関係式を求めてみる。
まず、各滑車の出入口のロープにかかる力は、滑車に種類よらず同じなので、非膣をFの力で引けば、下図のように各ロープにFの力がかかっていると考えられる。
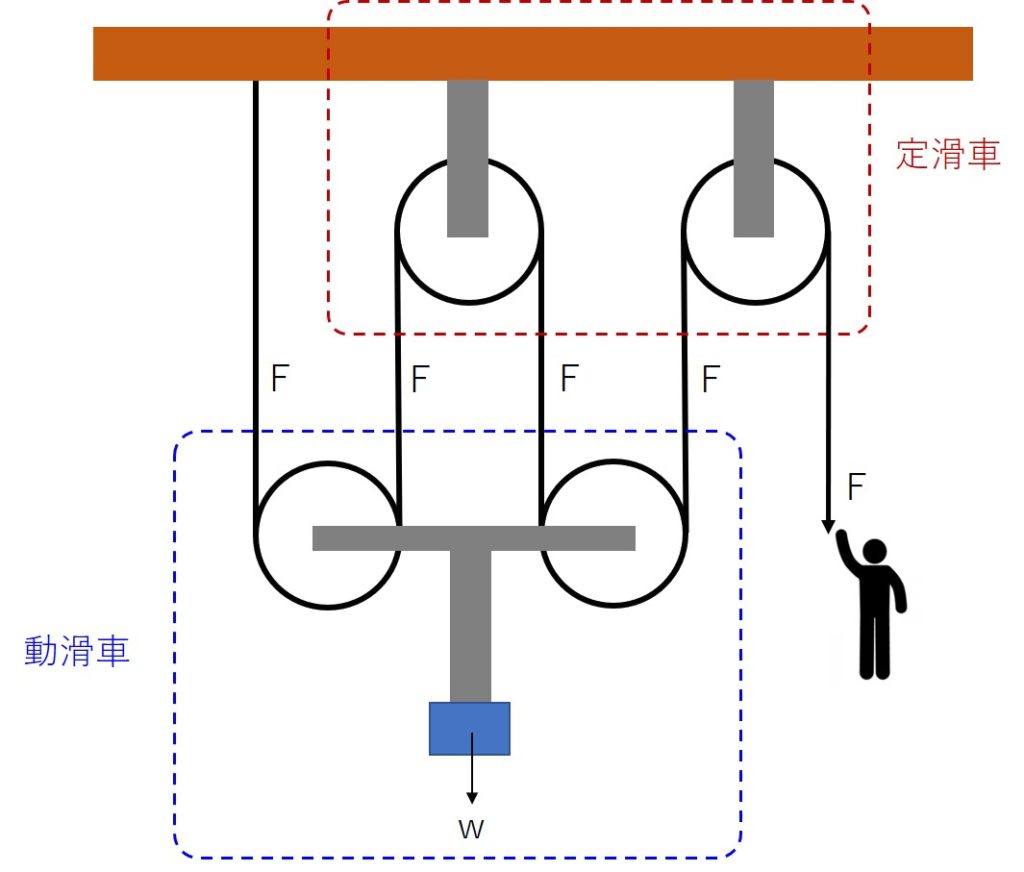
次に、滑車に働く力のつり合いを考える。今、二つの動滑車の軸には、力Wがかかっている。よって、各動滑車には、W/2の力がかかっている。向きは、向かって下側である。
ここで、先に示した動滑車のロープにかかる力と軸にかかる力の関係を思い出す。動滑車のロープにかかる力は、軸にかかる力の半分である。
よって、F = (W/2)/2 = W/4 とわかる。
例えば、重りW=20kg だったとする。このとき、上記のような機構を用意すれば、F=5kg で持ち上げらる。
話が長くなったが、滑車はこのように、持ち上げるという目的に対して、定滑車と動滑車を組み合わせることで、力を加える向きを変え、かつ、小さな力でそれを達成できるのである。
先のコロッセオの猛獣用檻のエレベーターは、上記のような仕組みを使って檻の重さに対して加える力を複合滑車機構で小さくして達成していた。
普段の生活では、滑車の威力を実感する人は少ないと思うが、現在のエレベーターも基本は古代と同じである。人類の素晴らしい発明の一つだと思います。
まとめ
- 滑車は、円盤の回転により、物を持ち上げる為の道具である。
- 定滑車と動滑車、およびそれらを組み合わせた複合滑車がある。
- 定滑車は、持ち上げるのに加える力の向きを変える効果がある。
- 動滑車は、加える力を半分にする効果がある。