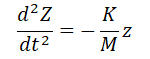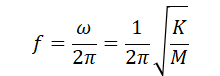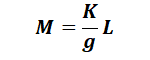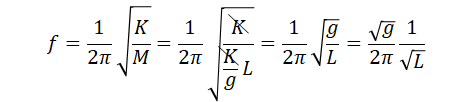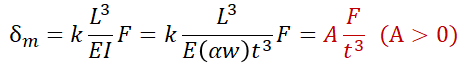〈前置き〉
本日は、Excelで連立微分方程式を解いてみたいと思います。解き方は、例によって、ルンゲクッタ(RK)法を持ちいます。「え?ルンゲクッタ法のような解の更新を含む数値計算って、Excelで出来るの?」と思われる方は、過去記事:Excelによるルンゲクッタ法の使い方 を参照ください。更新する際に、コピー&ペーストを繰り返すので多少手間ですが、解析ソフトなどがなくても解の様子を描画して確認できるので、安価でそれなりの予測をすることができます。正直、解の精度や収束時間が研究対象であったり、数万回以上の解の更新を必要とする方であったりしない限り、Excelでの予測である程度対応可能に感じます。
〈ルンゲクッタ法とは?〉
科学者や技術者は、新たな発見や創造のために、現象を予測することが求められます。その予測をする方法として、「微分方程式を解く」というのがあります。この微分方程式は、「知りたい量の時間変化が、どうなる」という具合に記述される式です。上手い具合に、「知りたい量=時間の関数」に整理できれば、後は好きな時間を入力することで、知りたい量の時間変化を知ることができます。これで、予測が完了です。しかし、そういう具合に式整理ができない物があります( 殆どの方程式は、こちらに属します )。そうした式を解く方法が、「数値計算法」です。これは、「ある規則で時間と知りたい量を更新し、方程式の姿を見出す」方法です。微分方程式の目的が現象の予測であるのならば、別に、明確な変数と時間の関係が分からなくても、傾向が分かる程度の関係が分かれば十分なのです。ルンゲクッタ法は、そうした数値計算法で一般的な手法の一つです。
〈数値計算の基本的な流れ〉
1.現象の数式化 ( 解きたい微分方程式をご用意下さい )
2.微分方程式の一階化( 時間と一変数だけの姿に変換してください。当然、式は、複数になってOK )
3.初期値設定
4.数値計算法で記述
5.必要回数まで更新する
〈Excelでのルンゲクッタ法の記述の仕方〉
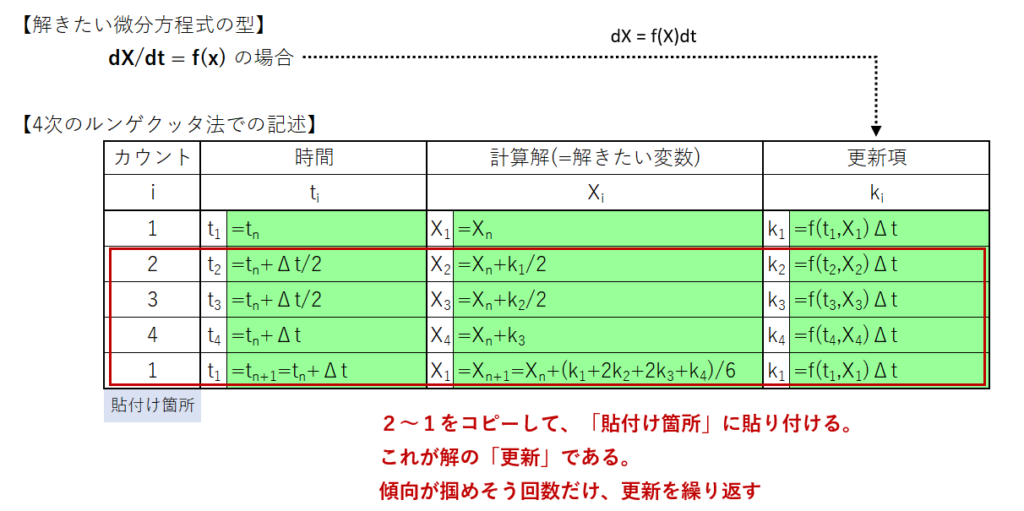
1.まず、「カウント、時間、計算解、更新項」の枠を作る。
2.次に、「カウント、時間、計算解」に数式を記入する。
・四次のルンゲクッタ法なので、一度に四つの計算を行う必要がある。
・カウントの初めの1は、初期値が入力される場所である。
・カウントの最後の1は、更新後の最初の値である。
・解きたい変数が増えると、計算解の列数も増える。( ex. 連立微分方程式 )
・計算解の列数が増えると、同じ数だけ更新項の列数も増える。
・更新項には、微分方程式をdX=f(X)dt の形に変換してf(X)Δt として記入する。
3.式が記入できたら、下図の赤枠箇所を丸ごとコピーして、同図貼付け箇所に貼り付ける。
4.傾向が掴めそうな回数まで更新して、カウントの1のみピックアップして、グラフ化する。
〈例示:連立微分方程式での記述〉
二次の微分方程式に関しては、過去記事にて具体例を示した。ここでは、連立微分方程式に関して記述してみる。題材としては、1927年にケルマックとマッケンドリックによって発表された感染症流行モデルである、ケルマック-マッケンドリック方程式 (KM方程式)を扱う。
1.微分方程式の記述

2.一階化 ⇒ 上図より、二階以上になっている式はないので、済。
3.初期値設定
ここでは、とりあえず適当に、下記とする。実際には、後で出てきた結果を見て、この項目を色々調整して方程式とそれが表す現象の理解を深めていくことになる。
3.ルンゲクッタ法で記述 ( 下図にNM方程式をルンゲクッタ法でExcelに記述したものを示す )
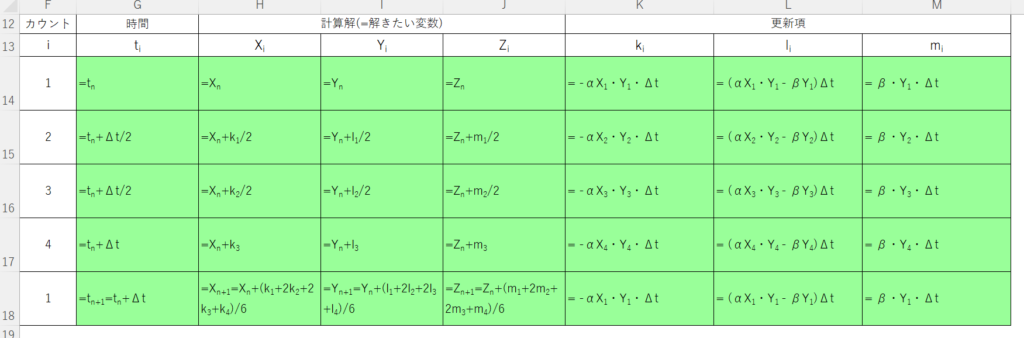
上図の緑色に塗られた箇所が、具体的に数値や式を記入する場所である。実際に計算するときは、緑色の箇所は、数値や、引用するセル番号の組み合わせで記述された式にすること。上図は、あくまでもその一歩手前の公式を記した。ここで、連立微分方程式が、どのように記述されるのかの理解を深めて頂きたい。
では、ここで、Excelで具体的に計算する形にする。まずは、文字式で示す。対応するセル番号で記述している。
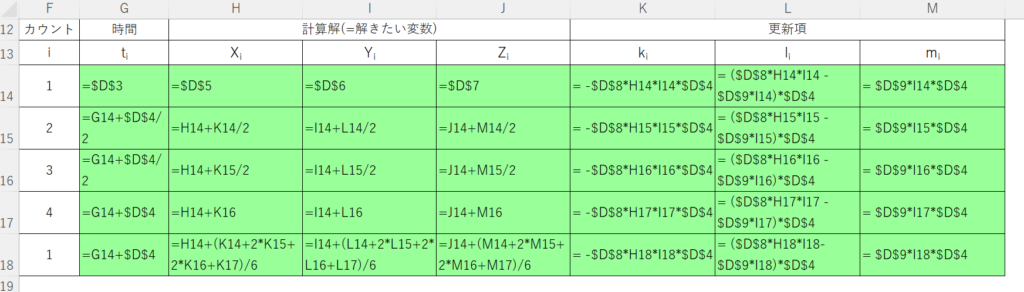
実際は、上図のように緑色のセルに文字を記入するとセル内に計算結果が表示される。つまり、4次のルンゲクッタ法の一回目の計算が完了したことになる。そこで、前述したように手動で更新(コピー&ペースト)を行うと、下記のようになる。
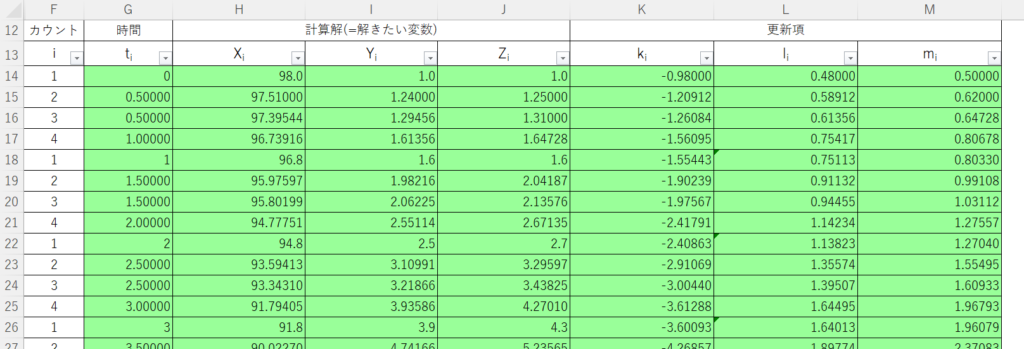
今回は、とりあえず一か月分の結果を見たいので、30回分( 30日分 )の更新を行う。
また、結果を見るときはカウント1の結果だけ見ればよいので、Excelのフィルター機能を使って表示を1だけにする。
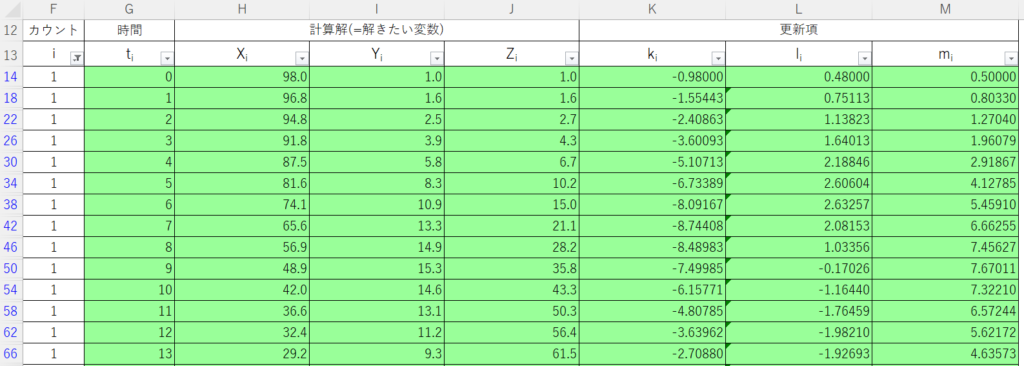
ここまで出たら、あとはExcelの描画機能を使ってグラフを作成してみる。例えば、時間と計算解を選択して、散布図( 平滑線 )を作図すると下記のようになる。
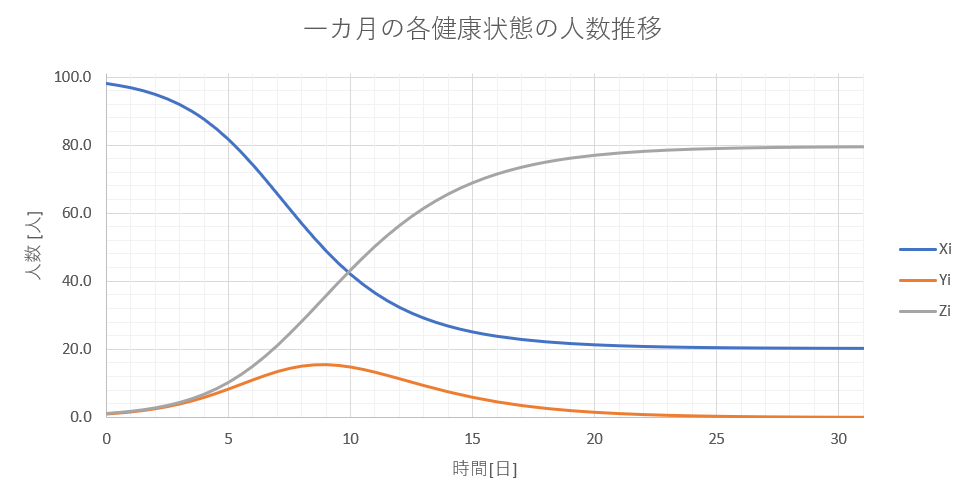
図. 一カ月の各健康状態の人数推移[ X ;健康者、Y ;感染者、Z ;除外者 ]( 感染率α=0.01、除外率β=0.5、組織総人数N=100人、初期健康者X0=100人、初期感染者Y0=1人、初期除外者Z0=1人)
この結果から、この感染症をかかった人が1人だけいると、健康な人の数は1W間で半減し、20日後には20人程度まで減少して落ち着く。また、感染者は、初め1人だったが9日後まで18人まで増加し、その後減少をはじめ、25日後には0人になる。つまり、このときこれ以後感染症に新規にかかる人はいなくなる。ところで、健康者の数が急速に減少し、感染者の数が増加しているとき、除外者の数が急上昇している。除外者は最終的に80人に達する。これは、何を意味しているのあろうか?除外者というのは、感染者そのものではなく、感染する恐れのない人である。例えば、ワクチンを接種して抗体を持った人、回復した人、死者、隔離者である。対象の現象によって、想定している除外者を議論することになるであろう。というのも、例えば、致死率100%の感染症ならば、上図で25日後には8割が死ぬことを意味しているので、感染者が25日後に0人になるからOKと楽観視できないからである。除外者の推移とその想定される内訳を議論することは、感染対策を議論することにつながるのである。例えば、除外者をワクチン接種者とすれば、その接種率を8割にすれば、感染症を抑えることができる。。となるのである。KM方程式は、ネットで検索すると様々なモデルが提案されているので、是非読んでみると面白いと思う。感染率と除外率がどういう関係性の時に、感染が収束するのか、爆発するのかなどが予測されていたり、、感染症に対する方程式とそのパラメータの整合性を考察したりした論文が多数ある。
さて、本日は、Excelで連立微分方程式をルンゲクッタ法で解く方法を紹介しました。大学や大学院の研究室で非線形現象を扱っている方は、連立微分方程式を解くことが多いと思います。MATLABなどの数値計算ソフトで解いても良いですが、Excelでもある程度のことは伝わったと思います。是非、参考とする論文やデータがある場合は、その式とパラメータを入力して解いてみてください。今回のKM方程式も、ローレンアトラクタのように、「個別の解を見るとカオス状態だったのに、全体をみるとある挙動の中で収束する」傾向が確認できるかもしれません。
では!
(参考過去記事): グラフ化の方法など記載しています。