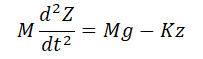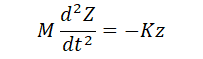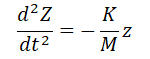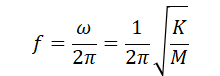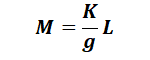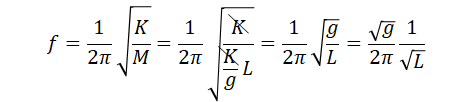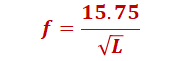電気製品の設計をしているとき、「この製品の固有周波数は、どのくらいだろう？何かの振動の周波数に近くて、共振したりしないかな？」と疑問に思うことがある。

特に、スピーカーを搭載していたり、振動する環境下で使われる製品ならば、尚更である。そんなとき、設計した製品の固有周波数を概算する、多分有効だと思われる簡単な方法を思いついたので、ここに記すことにした。多分、振動体を専門に扱っている技術者ならば、常識も常識だと思う。だって、高校物理程度の知識だから。。

【設計中の製品の固有周波数を概算する方法】

まず、製品の固有周波数とは何か？を少し考えてみる。

製品には、沢山の部品が使用されており、その全てに固有の周波数がある。製品の周波数分布は、それらの各部品の周波数分布の合成である。さて、その製品は、一般的には、ある平面に乗せて使用することが多い。ということで、一般的に製品は、平面との接触面に、「ゴム脚」などの弾性体を配置する。このゴム脚が、製品の自重で微妙に沈み込み、製品の位置が安定する。これは、重りを吊るしたバネが安定する現象と同じである。重りを少し押し下げ、手を離せば、バネは安定位置を中心に上下に振動する。このことから、一般的な製品の振動現象は、まず、外界の物品と一番に接触する弾性体に着目し、その固有振動を考えれば良いと分かる。

では、早速考えてみる。今、下記のような電気製品があるとする。

図1. プロジェクタを平面に置いた状態

先ほど説明した、ゴム脚が、微妙に歪むので、それを誇張して表現してみる。

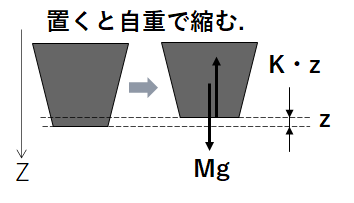
図2. ゴム脚が製品の自重で変形しつつある様子のイメージ

ここで、運動方程式を立ててみる。運動方向としてZ軸を図2のようにとる。製品重量をM[kg]、微小変形量をz[m]、ゴム脚のバネ定数をK[N/m]とする。

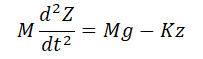
・・・(1)

今、着目しているのは、ゴム脚の微小な弾性なので、場の力Mgの影響は小さいから、無視することにする。すると、

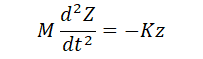
・・・(2)

となる。両辺をMで割ると、、

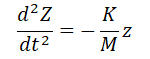
・・・(3)

となる。ここで、(K/M)は、固有振動数ω[rad/s]の二乗である。ωは、ω=2πf という関係式があるので、、、

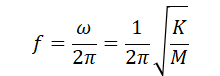
・・・(4)

と言う具合に、固有周波数f[Hz]の式が導ける。ところで、図2において、ゴム脚が自重で変形しきったときの変形量をL[m]と置く。設置面からの反発力(垂直抗力)をN[N]とすると、つり合いの式は、、

N=Mg-KL

・・・(5)

となる。ここで、製品が振動するときのことを考える。ゴム脚が変形する瞬間では、垂直抗力N=0と考えられるので、

Mg＝KL

・・・(6)

とできる。(6)式から、

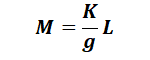
・・・(7)

と近似できる。この式を、(4)式に代入すると、、

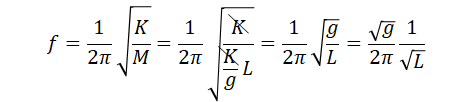
・・・(8)

となる。電気製品の設計現場では、一般に、単位は、ｍよりも、ｍｍをよく使うので、単位変換をすると、、

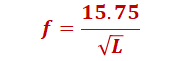
L：ゴム脚の変形量[mm]

・・・(9)

と言う具合に、固有周波数が求められる。(9)をみると、製品重量Mやバネ定数Kが消えている。従って、単純に、ゴム脚一つの変形量Lのみに着目するだけで、製品という系の固有周波数を概算することができる。

ここで、こんな近似使いまくって、計算結果が信頼できるのか？と思われるかもしれないが、、ここでは、「想定使用(試験)下の振動条件と、計算で求めた系の固有周波数が近いかどうかを知り、設計方針を立てることを目的としているので、近似計算の結果で十分」だと私は思っている。設計方針というのは、例えば、「固有周波数を概算して、それが振動条件の周波数に近ければ、、ゴム脚の硬度、形、大きさを変えたりして、Lを調整しよう。試作のときに検証できるように、複数パターン作っておこう」という思考のことをさす。

電気製品の設計の現場において、製品の固有周波数は、恐らく、やってみないと分からないという感じが多いと思う。しかし、やってみた結果、悪い方に転んで焦るよりも、ざっくり予測して、複数パターン準備しておく方が、良いと思うのである。是非、活用に向けて一考いただけたらと思う。

【本日の動画】河岸段丘から相模川に流れ落ちる水と音

滝とは言いませんが、激しい流れです。その姿を見て、音を聴いていると、雑念が消えていくような、そんな感じがします。自然に触れることの素晴らしい効果の一つだと思っています。

今日は、人をみるということについて呟きたいと思う。

日々生きていると、何十、何百、と言う人と出会う。知人がおり、友人がおり、家族がおり、ときに恋人がいる。

学生は、毎日、クラスの友達、先生、部活の仲間に出会う。

婚活や恋活、意図的な友達作りをしている人は、それなりのコミュニティに参加したり、アプリを使ったりするので、毎日、何十人という異性と出会うであろう。

社会に出て仕事をする人は、毎日、チームや得意先と出会い、、毎日、多くとも20人弱と関わるであろうか。

このように、我々人間は、日々、他人と関わって生きているのだが、今まで生きてきて、多くの人が人をちゃんと見ていないと良く感じ、本日のこの記事を書くことにした。何も、私が承認欲求が強く、認められてこなかったから、この記事を書くわけではない。

「物事をちゃんとみる」とは、どういうことであろうか？

それは、今、自分の目の前にある物や事を、自分の五感で捉えるということである。それが、良く知っている物や事ならば、捉えなおそうとするということである。

なぜ捉えなおす必要があるのか？それは、物事の今をちゃんとみて、真剣に向き合うためである。まして、それが人相手ならばなおさらである。

私は、人は三日で別人になれると真剣に思っている。学生であれば、三日前には明らかに間抜けだった奴がテストで良い点をとったり、恋人ができて素敵な経験を経て一気に所作に余裕をみせるようになったり、三日間で仕事に必要な知識を習得し会話についてきたり、、そんな経験をしたこと、そんな変化をした者を、数多くみてきたからである。また、三日前は元気で、今はこの世にいないとか、、三日前は幸せだったのに、今は鬱になっているとか、そんな変化も目の当たりにしてきた。

今、人も世の中の変化も、速いのである。こんなとき、意識的に、捉えなおすことをしなければ、本質を見落としやすくなるのは当然である。

せっかく大人になり、自信を深め、物事にチャレンジしようとしている男がいたとして、、その変化に気が付かず今まで通りに子供のように接したら、それこそ失礼であり、、せっかくのパートナーを失うことになるのである。

せっかく自己研鑽をした人がいても、その成長を探ろうとせず、今まで通り接していたら、宝も腐ってしまう。まずは、毎日、毎瞬、出会う度に、、会話の中でその人を捉えなおそうとして欲しい。きっと、相手は喜ぶし、それは、あなたに幸運をもたらすことは間違いない。

数年前に興味がないとして振った異性だが、今目の前で会話していて、捉えなおしたらあれ？と思うこともあるのである。もっとも、この話をしていて思うのは、「ちゃんと捉える」とき、「自分の記憶」と照合するのだが、その記憶が常に変動していることに注意が必要だということであるが。。。

私は、毎回、出会う人、会話する人、メールする人、、真剣に捉えなおしています。とても疲れることだけど、とても楽しく、ときに(知りたくないことも気づいてしまって)辛く、全体的に素晴らしいことだと思っています。

では。

【本日の動画】ハングリースパイダー

(捕食者である)蜘蛛が、(獲物である)蝶に恋をする物語です。好きなあの子を、生きるために食べるべきか、あの子の幸せを考えて逃がすべきかに葛藤する蜘蛛の心を描いた歌です。逃がしたとしても自分の恋心は報われず、蝶は自分を敵としてしか捉えず去っていくのみ。しかし、情をかけずにはいられない蜘蛛。。何と言う情景であろうか。。美女と野獣は、美女が野獣の本質を理解したからこそ、そこに愛があり、野獣の献身と悲哀、そしてハッピーエンドが見る者を幸せにしてくれた。しかし、蜘蛛と蝶は、、、。内面を理解すること、その重要性を気が付かせてくれる、麻薬のような名曲です。

私は、機構設計という分類のエンジニアである。

材力、工力、流体力学、回路、熱、統計力学といった知識を駆使して、製品を成立させる形状や機構を作るのが仕事である。簡単に言えば、製品を目に見える姿にするのが仕事である。今を時めくソフト設計者は、機構設計者が作った物に、命を吹き込む役割である。これもまた、重要な仕事である。

本日は、こうしたエンジニアが、業務上の問題を解決するときにやるべきことを申し上げたいと思う。

それは、「問題をしっかり把握し、原因仮説を立て、個別に対策法を立案する」ということである。

こんなことは、当たり前のことなのだが、実際に、それなりの大手と言われる会社で何年も働いていて思うのは、この当たり前のことができない人がほとんどなのである。

本日、私か申し上げたいことは、これで終了である。ただ、話を終わる前に、「この当たり前のことをやっていない殆どの人は、どうやって対策してきたのか？」を示したいと思う。自分が、そうなっていないかを自問してもらうためである。

【多くの人の問題対策の仕方】

　過去の類似した成功体験を思い出す ➡ ( その「仕組み」を理解せず )対策を実行する

このアプローチの良くない点は、二つある。

① 目の前の問題を、分析していない。

そのため、成功体験における問題が、直面している問題と等価か分からない。

よって、対策が的外れになる可能性が高い。失敗してしまったら、また類似例を記憶から探せばよいと言うかもしれないが、そんなに沢山の記憶を引っ張り出せる人は中々いない。ベテランでもそうである。それができる人がいる職場は幸せだか、それはまれだと思った方が良い。大抵は、皆、沈黙である。

② 成功体験が何故成功したのかの仕組みが、分かっていない。

そのため、対策が失敗したときに、なすすべを失う。このとき、失敗した事実を元に、思い付きのCUT＆TRYを積み上げて結果を出す方法もあるが、これでうまくいことは中々ない。上手くいったとしても、予想外の時間とお金を費やすことは確実である。

こうならないようにするためには、「問題を分析し、原因を仮説立て、対策案を立てる」という思考を、大学受験であったり、大学や大学院の研究を通じて多くの人は学んできたはずなのだが、いざ、実際に取り組むとなると、何故か出来ないのである。

本日申し上げたことは、実は、ベテラン社員が良くやりがちなことである。ベテランになると、経験が沢山蓄えられてくるので、無意識にそれを過信し、その中で解決しようとするからである。そんなとき、その成功対策の原理が分かっていて、かつ問題が過去の成功体験と等価であると分かる場合ならば良いのだが、、同じような課題に対してベテランでも、、若輩と同じく、むしろそれ以上に問題解決に難儀している姿を多く見てきて、ああ基本を疎かにしているんだなと、確信をするのである。

【本日の動画】高麗川のせせらぎ

最近、少し体調を崩しており動画の撮影に行けていません。少し前に行った、高麗川のせせらぎです。ボーっと眺めていると、眉間の左側が何だかムズムズしてきます。

会社で、仲間と仕事をしていく上で、意思疎通は大事である。しかし、会話がスムーズに進む人とそうでない人がいる。こうした状況を数多く経験してきて、その原因の一つは、双方の精神年齢とIQの差が大きく関係しているのではないかと思い、つぶやくことにした。。

職場での意志疎通の成立に影響すると思う要素

① 精神年齢

② IQ

本日の話は、上記の視点を前提に展開する。①は思慮深さ、胆力のことをさす。②は頭の良さのことをさす。私は、共に仕事をする者同士が、この①と②の観点から、どの組み合わせのときに意思疎通がうまくいっているかを、自分の経験と他人の観察によって、整理してみた。下記の図1～3で示す。

( ※ 当然、 一般性はない。あくまでも参考意見に留めて頂きたい。 )

図１. 共同労働者同士の精神年齢とIQの高低による意思疎通の成立感１

チンパンジーのIQは、一説によると50程度である。人間で極度の低IQと呼ばれる者は、70程度。チンパンジーとの差は、20ほどだが、人は言語を操り、記憶、計算、推論を行うことができる。何を言いたいかと言うと、IQ20程度の差は、感受できる世界、できることが大きく違うということである。なお、人で言えば、89以下は低IQ、90～109は普通、110以上は高IQである。先のIQ20の差を適用するならば、高IQと低IQは意思疎通が成立しない。この観点から、まず、意思疎通の成立性を〇×△で示した。

ここで、精神年齢という概念を持ち込む。精神性の高い人は、共に何かをしようとすると、歩み寄りの姿勢を見せる。賢い者は、相手に伝わるように会話の程度をかみ砕き、平易な表現で言い換える。一方、知能の劣る方は、分からないなりに思考を行い、相手との理解の差を埋めようと努力する。この双方の歩み寄りにより、単純なIQ差で会話が成立しなかった者同士が、会話できるようになる。図2にこの歩み寄りの概念図を示した。

図２．「歩み寄り」が、意思疎通におけるIQ差を縮める概念図

これは、言語とイメージを操る人間だからできることである。こうして、図1に見られるように、双方の精神性が高まるにつれて、意思疎通の×が△に、△が〇になる場合があることを表現した。

図３. 共同労働者同士の精神年齢とIQの高低による意思疎通の成立感２

図３では、IQと精神性がそれぞれ一ランク異なる者同士の意思疎通の成立感を示した物である。先ほどの、IQと精神性が高くなることで見られる歩み寄りの姿勢により、表現した。上位の知能、低精神年齢の者は、基本的に下位の知能の者と共同作業ができないので、要注意である。

以上の考え方に従って、図1や2で表現されていない関係も考えてみて欲しい。職場で自分が意思疎通しにくい人と自分の立ち位置が分かり、気持ちが整理されることを期待しているからである。そうすれば、接し方を考えやすくなるとおもうのである。

【本日の動画】鎌倉のとあるお寺

のんびりお散歩を楽しんできました。時間が早かったので、あまり人もおらずよかったです。カエルの合唱、鳥の美しいさえずり、、何とも心が落ち着きます。こうした風情を感じられる鎌倉は、素晴らしい場所だと思うわけです。。

今日は、前回に続き、数式の遊びを紹介する。テーマは、熱設計である。

熱設計とは、「製品開発において、物を作る前の構想時点で、熱源が冷えるような機構を考えること」を言う。この概念を知らず、モノが出来てから、筐体に孔をあけたり、適当なヒートシンクを持ってきて取り付けたりでは、昨今の高発熱密度な製品や部品を冷やすことは不可能である。

一重に熱設計と言っても、やり方は、問題設定によって様々である。

Q1：筐体内に、発熱量P[W]の熱源がある。これを何か特別な機構で排熱する必要があるか？

Q2：Q1で排熱する必要がある場合、どれだけの流体を当てればよいか？

Q3：高発熱密度な部品がある。この熱をある領域まで広げたい。どうする？

Q4：ある熱源がある。風が一方向から吹いている。これを冷やすには、どれくらいの空間と風量、ヒートシンクがあればよいか？

などなどである。

本日は、Q4について、一つのアプローチ方法を紹介する。大学、大学院で研究活動をしたことのある方は、必ず、最適化問題を何らかの形で触れたと思う。

本日紹介するQ4へのアプローチを理解した上で、是非、この方程式を、特定の量に対して最適化する方法を考えてみて欲しい。。それはきっと、あなたが真のエンジニアや研究者になったときに、問題を解決する素晴らしい力の源になると思うからである。また、是非、私にもそれを教えて欲しい。

【問題Q4】

ある熱源がある。風が一方向から流れている。この時、熱源を冷却するには、どれくらいの空間とヒートシンクがあればよいか？ただし、熱源の熱は、ヒートシンクに全て移動できるとする。また、ヒートシンクのフィンの加工上の制約条件は、無視しても良い。

********************************************************************

まず、条件を整理、仮定してみる。

◎ 熱源 ⇒ 発熱量 P[W]、目標温度 Tt[℃]、周囲環境温度 Ta[℃]

◎ 風 ⇒ 風量 Q[m3/min]

◎ 空間サイズ ⇒ 流路サイズと考える。

　・流路幅 W[mm]

　・流路長 L[mm]

　・流路高さ H[mm]

◎ ヒートシンクサイズ

　・FIN幅 ω[mm]

　・FIN間距離 δ[mm]

　・FIN数 n[枚]

　・FIN長 L*[mm]

　・FIN高さ H*[mm]

次に、これらを図示してみる。問題は、情報の仮定と整理をし、図示することで、より理解が深まる。これが「数式遊び」の極意であると、私は思っている。

図1. 熱源と周辺空間(流路)の関係イメージ

ここで、問題で問われている、ヒートシンクについて考えてみる。ヒートシンクは、流路の中に位置する部品である。また、ヒートシンクは、流路に対して水平かつ短冊状にFINが配列される部品である。よって、例えば、下図のように仮定してあげれば良い。つまり、流路をヒートシンクのFINで刻んでやるのである。

図2. 流路にヒートシンクを配置したイメージ

図2では、流路長L、流路高さHが、それぞれ、FIN奥行きL*、FIN高さH*と等しいとした。

さてこのように図化すると、例えば、以下のように、「熱源情報、寸法情報、風量」に関する関係式 を立式することができる。

1). ヒートシンクサイズに関する関係式

• 放熱面積：S = n × ( 2HL ) [mm2]　・・・①
• 包絡体積：V = WH = { nω + ( n+1 )δ }H [mm2] ・・・②

FIN数 n[枚], フィン高さH[mm], FIN奥行き(=流路長)L[mm]

ヒートシンク幅(=流路幅)W[mm], FIN幅 ω[mm], FIN間距離 δ[mm]

2). 熱伝達率hm[W/(m^2・K)]の定義式 と熱抵抗値R[K/W] の関係

• hm =　P/{S・(Tt – Ta)} = P/(S・ΔT) [W/(m^2・K)] ・・・③
• R = (Tt – Ta)/P = ΔT/P [K/W]　・・・④

発熱量P[W], 目標温度Tt[℃], 周辺空気温度Ta[℃]

hm = 1/(S・R) [W/(m^2・K)] ・・・⑤

ここで、放熱面積Sの単位は、ｍｍ2 とすることが多いので、⑤式もそのようにしておくと便利である。つまり、

hm = 10^6/(S・R) [W/(m2・K)] ・・・⑤’

である。

なお、この式において、風が熱を空気中に移動させる能力である熱伝達率が分かっていれば、どれくらいの放熱面積が必要かが分かる。⑤’式を変形すると、、

S = 10^6/( hm・R ) [mm2] ・・・⑥

となる。少なくとも⑥式以上の放熱面積を取れば、よいと目算ができる。

• S ≧ 10^6/( hm・R ) [mm2]・・・⑦

3). 強制熱伝達率hmf [W/(m^2・K)] の関係式

• hmf = 3.86×(U/L)^0.5 [W/(m^2・K] ・・・⑧
• Q = AU [m^3/s] ・・・⑨

⑧式は、熱設計関係の書籍でよく登場する式である。論文などを見ると、条件別に色んな式があるので、適宜参照してほしい。。が、熱設計指針をざっくり立てるのが目的なら、、正直、この関係式だけ覚えておけば良い気もする。

⑨は、流体力学の初めの方に登場する、連続の式である。流路内において、流路断面積A[m2]と流速U[m/s]の積が一定というものである。⑧式に⑨式を代入すると、、、

• hmf = 3.86×{ Q/(AL) }^0.5 [W/(m^2・K)] ・・・⑩

　風量 Q[m3/s], 流路断面積 A[m3], 流路長L[m]

となる。ここで、流路断面積Aは ｍｍ２で、風量Qは m3/min で考えることが多いので、これをQp[m3/min]として⑩式に代入する。

• hmf = 3.86×{ Qp/( 60AL )×10^8 }^0.5 [W/(m^2・K]　・・・⑩’

　風量Qp[m3/min], 流路断面積A[mm2], 流路長L[mm]

以上の式から、⑦式と⑩’式を、hm = hmf とし、さらに⑦式に①式を代入すると、、「熱源情報、寸法情報、風量」に関する関係式 が導かれる。

S ≧ 10^6/[ 3.86×{10^8×Qp/(60AL) }^0.5 ]

↔

2nHLR ≧ 10^6/[ 3.86×{10^8×Q/(60AL) }^0.5 ]

式を整理すると…

• QL×(nHR)^2/A ≧ 6,350 ・・・⑪

となる。ここでさらに、流路断面積A ＝ (n+1)δ×H なので、⑪式に代入して整理すると、、

• QHL×(nR)^2/{δ(n+1)} ≧ 6,350 ・・・⑫

となる。

後は、これに確定している量を代入して、欲しい未知量を求めれば良い。

例えば、良く開発現場で、この熱源を冷やすのに必要な空間とヒートシンクサイズを見積れと言われる。驚いたことに、使用できるFANが決まっていることもある。この場合、仮に、Q = 0.1m^3/min, R =1K/W とすると、、⑫式は、

HL×n^2/{δ(n+1)}≧63,500

を満たせば、何でも良いとなる。。さて、あなたは、これにどう答えるであろうか？？変数は、4つである。如何にすれば、最適といえるであろうか？？

定石は、変数の変域を定義するのである。。。が、開発現場では、これを否定されることの方が多い。理由は、(熱設計者が)変域を定義し、(承認者らが)それを許容して、最悪の条件が導かれたときに、(承認者らが)プライドが傷つくのを恐れてGoサインを出せないからと、かねがね感じている。話を戻して、変域を定義してみる。

例えば、

・1 ≦ H ≦ 30mm

・1 ≦ L ≦ 50mm

・1 ≦ W ≦50mm

・ω≧0.3mm

・δ ≧0.6mm

・n ＞ 0

とする。Wは、ωn+δ(n+1)という具合にFINとの関係が深いので先にこちらを考える。W≦50mm より、、

0.3n+δ(n+1) ≦ 50mm 

である。δ＝0.6mmとすれば、0.3n+0.6n+0.6=0.9n+0.6≦50 なので、

n ≦ 54.8 ( ただし、δ = 0.6mm, ω = 0.3mm )

ここで、HとLの関係に式を詰めていく。

HL×54^2/{0.6(54+1)}≧63,500

↔ HL≧ 718 (1≦H≦30, 1≦L≦50)

このことから、最小のHとLは、HL=718の境界上の任意の数で良いので、、例えば、(H,L)=(14.36, 50) となる。

まとめると、熱抵抗値R＝1K/W、風量Q＝0.1m3/min の風が流れる流路において、フィン間距離δ=0.6mm、フィン幅ω=0.3mm、流路幅W＝50mmとして、フィン数n=54枚 とすれば、、最小のフィン高さ(=流路高さ)H=14.36mｍ、最小のフィン奥行き(=流路長)=50mm と算出できる。。(あれ、あってんのか)。。色々課題を思いつきましたが、、、今日はここまでにしたいと思います。。

では。。

【本日の動画】相模川の水の煌めき

激しい流れに、太陽の光が反射し、キラキラ煌めいております。見ていると、雑念が払われて、スッキリしてきます。