物理学などの学問は、その扱う対象のサイズによって、分野が分かれている。
例えば、「水の流れ」を例にとってみると、、、
◎ 目に見える水の流れ → 「流体力学」で記述
◎ 水分子の働き→ 「分子物理学」 で記述
◎ 原子や原子核の働き → 「原子核物理学」で記述
◎ 核子やクオーク の働き → 「素粒子物理学」で記述
という具合になる。
同じ対象を見ているのだが、みるサイズによって考え方が違うのである。
しかし、それぞれの学問がつながっていなければならない。何故ならば、サイズという制約を除けば、同じ対象をみているのだから。そこで登場する概念が、「くりこみ」である。
この「くりこみ」というのは、下のスケールの学術的効果が、上のスケールで記述する際に、係数や定数の値に反映されることをいう。
従って、例えば、あるスケールの学問で、Y=k・X ( k:係数 )という式が成立するのならば、そのkには、その下のスケールの学問からの贈り物が含まれているのである。
このことを意識することが、今の企業の工学的アプローチを進化させることにつながると私は思っている。
というのも、機構設計をする際に、強度や冷却のために、「材料力学」「流体力学」「熱設計」に関する計算を行うが、それらは皆、目に見えるスケールでの学問の話であり、下のスケールの学術的効果については深く検討されていないからである。
例えば、熱設計を行う際に、熱伝導に関する下記の重要な式がある。
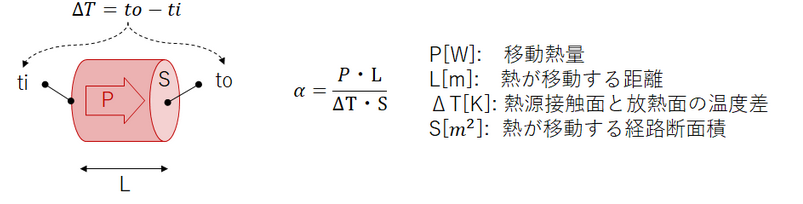
上記のαを「熱伝導率」という。物体固有の値であり、熱設計を行う際は、「定数」として扱う。
私が言いたいのは、「これが本当に定数なのか?」を疑い、そこに「くりこまれている下のスケールの効果」を見直す必要があるのではないのか?ということである。
特定の条件、例えば、「温度、力(電磁気力・音圧etc)、分子構造、イオン構造」などをが少し違うだけで、値が変わったりすることはないだろうか?
例えば、アルミの板があって、その形状に特徴があったり、表面が化学反応していたり、別の微粒子が含有されていたり、空間を超えて作用する力が働いていたりしたときに、、、アルミの熱伝導率は、やはり同じなのであろうか?
私は、「等温下で熱伝導率を変えられる手法」が見つかると、電気製品で出来ることはもっともっと増えると思っている。高密度に集積させたチップを上手く冷却できるからである。
私は学者ではないので、ここら辺に踏み入る余裕がないが、ここら辺に答えてくれる学術研究成果の誕生を期待したいと思う。
【本日の自然動画】
相模川の流れに太陽光が当たってできた、光の筋です。画像が荒い場合は、youtubeの再生画像が低画質になっている可能性があるので、HDにしてお楽しみください。