回帰分析というのをご存知であろうか?これは、二つの量の関係性を分析する手法である。手法としては、今現在、人類が見つけている最も効率的な方法論である。比べる量が三つ以上ある場合は、重回帰分析という。今日は、Excelで簡単に回帰分析する手法を紹介する。身近な現象、実験に使ってみてほしい。
Excelでどうやるのか?
例えば、下記のようなデータがあったとする
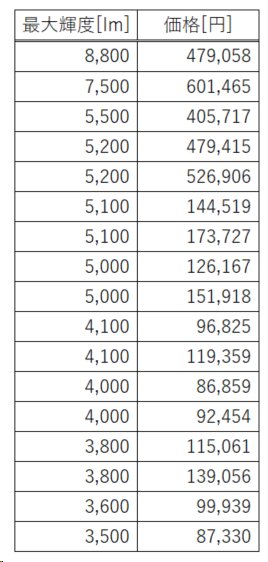
これは、某R社のプロジェクターの輝度と販売価格を表にしたものである。データは、価格.com ( 2019/2現在 )のデータを元にした。例えば、あなたが、R社の競合会社の企画者であったとして、「明るさ(輝度)と販売費用の関係」を知るにはどうすればよいだろうか?
こうしたときに、結果の正当性はいったん置いといて、人類の見つけた最善の手法が回帰分析である。
まず、Excelを立ち上げ、上表を打ち込む。そして、表題から表の下端まで、下図のようにマウスでドラッグする。
次に、Excelのリボン(コマンドの上側に出ている部分)において、「挿入」を選ぶ。

この「挿入」の中の中央に、グラフという項目があり、下図の赤丸箇所をクリックする。
すると、下図のようなグラフが出力される。これを散布図という。
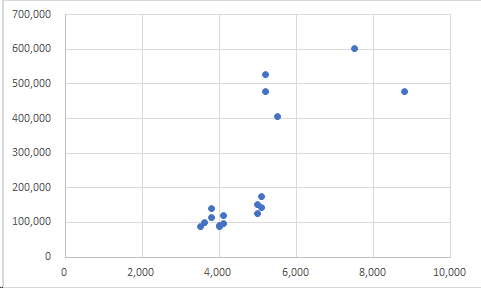
この時、横軸が表の左側、縦軸が同右側である。解析の際は、縦軸と横軸を明確にすることは極めて重要なので、記載しておく。やり方は、グラフ上にマウスのカーソルを持っていくと下図のように「十字」「ペン」「ジョウロマーク?」みたいなものが右上に出てくる。その十字(赤丸)をクリックする。
すると、下図のように「グラフ要素」が出てくるので、「軸ラベル」に印を入れる。
すると、下図のようになる。
ラベルのところをマウスでクリックし、要素名を記入する。
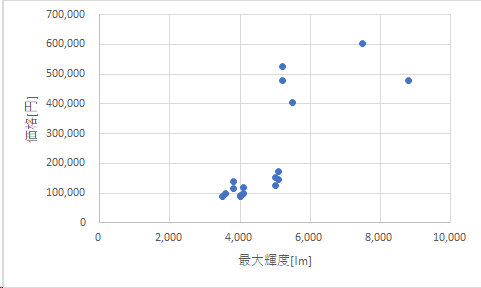
ここで、回帰直線を引く。これは、各点からの距離和が最小になるように引かれた直線である。人類が複数の点間を通る線の引き方として見つけ、定めた、最善の方法である。これに対して否定できる人は、今のところいません。(数学者ですらできていないから)
やり方は、上図において点のどれかにカーソルを合わせてクリックする。
そして、マウスをその場で右クリックし、「近似曲線の追加」を選択、クリックする。
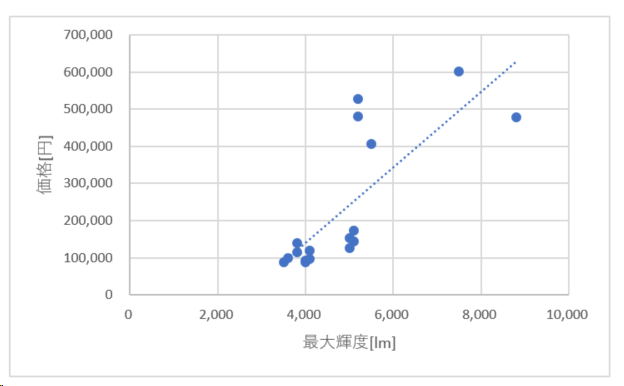
グラフの点線が、回帰直線である。後は、この直線を表す関数が分かれば、「輝度と価格」の関係が予測できたことになる。やり方が正しいのであって、予測精度などの結果が現実に正しいかどうかは、別の話である。
さて、やり方は、上図の回帰直線を先ほどと同じく、クリックする。出てきた小コマンドの「近似曲線の書式設定」をクリックする。すると、Excelの右側に新たなコマンドが現れる。
そして、右下の赤で囲った箇所「グラフに数式を表示する」にチェックを入れる。そうすると、グラフ上に、数式が表示される。これが、データから回帰分析によって得られた、輝度と価格の関係である。
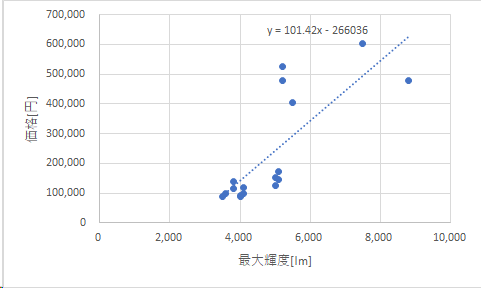
この後、さらなる分析やディスカッションを経て、この予測が使えそうだと合意ができたら、Excelで下図のようなフォーマットを作っておくと、何かと便利である。
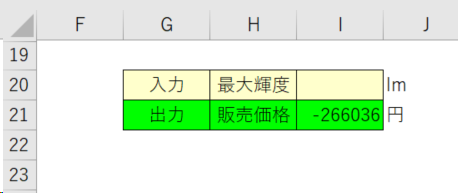
入力の空欄(=セルI20)は、今後、好きな輝度を数値で入力する箇所である。
出力の空欄(=セルI21)には、先ほど求めた回帰直線の数式を記入する。

先ほどのグラフ上の数式におけるXは、最大輝度の入力値である。上図の場合、最大輝度を入力する箇所はセルI20なので、Xの箇所にI20と記述する。
例えば、最大輝度7,000lmのプロジェクターを企画することになったとき、販売価格はどのくらいを想定すればよいか?と思ったとき、上のフォーマットに7,000と入力すると、

という具合になる。
この結果が、予測結果として十分かどうかは、別途議論が必要である。
例えば、この予測では、2,000lmなどは価格がマイナスに出てしまう。この場合は、データ収集箇所を変えてみたり、近似曲線の直線ではなく他の関数を選んでみたり、比較するデータ自体を変えたり、別の要素を追加したり(=重回帰分析)など、まだまだ手は沢山あるので、今後少しづつ紹介していく。
まずは、手持ちのデータから何か語れ!予測しろ!と言われたときに行う、最も一般的な科学的手法を紹介した。是非色々使ってみてほしい。
まとめ
・二つのデータから関係性を求める最も一般的な手法が回帰分析である。
・データ⇒散布図作成⇒近似曲線(回帰直線)作成⇒数式表示 (⇒ 入出力フォーマット作成)
・やり方が正しいのであって、結果が正しいことを保証するものではない。
式ができたらテスト、現実にそぐわない場合は、前提を見直そう。