機構設計者として、日々仕事をしていると、色んな問題に直面することになる。
Q: こんな構造は、どうやって作るのか?
- 材料は?
- メカニズムは?
- 強度は?
- 時間変化は?
- 入手性は?
- コストは?
- 加工性は?
- 組み立て性 は?[量産性]
- 法律は?
- 管理は?
- その他…
熱設計者なら、
Q: この筐体サイズの中に、こんな発熱部品があるのだが、部品は使えますか?
- 筐体サイズは?
- 部品サイズは?
- 部品毎の発熱量は?
- 部品毎の目標温度( = 動作保証温度 )
- 使用環境は?
- 騒音値の制限はあるか?(=強制空冷ができるかどうかに関わる)[静音性]
- それで冷えるの?[冷却性]
- もっと小さくできないの?[小型化・薄型化]
- もっと軽くできないの?[軽量化]
- 金属なら回路部品との絶縁を取らないといけないけどどうすんの?[絶縁]
- コストは?もっと下げられないの?[ロウコスト]
- 加工性は?
- 組み立て性は?
- 入手性は?
- 法律?
- 管理?
などなどである。
熱設計の場合は、開発開始時点で、筐体サイズが決まっていなかったり、内部に搭載する部品の種類、数、サイズ、発熱量が決まっていなかったりする中で、常に、上記の質問を問われ、必ず「最適か?」という質問が副えられる。しかも、要求事項の全体像が分かっていない無能な企画者が多いと、設計者が見積もりを出すために「条件設定、定義」をすることすら否定される。。。
この状況に対して、一般的な理系の大学教育を真面目に受講した者ならすぐに分かるが、「条件設定が禁止された関数の最適化は、不可能」なのだが、そこが分からないのである。勉強はしっかりしましょう。思うだけで、技術の積み上げを超越した物ができるほどの技術を、我々人類はまだ手にしていないのですから。。
さて、前置きが長くなったが、、機構設計者は、上記のような多くの質問に常に答えなければならないのである。これらは、侃々諤々(かんかんがくがく)とした議論を続けていても、全く答えは出ない。計算をするか、実験をしてデータを元に推論をしていくかでしか、答えは出ない。実験は、基本的に試作をして行うので、お金と時間がかかる。いずれも有限なものですから、大切にしなければならない。そこで、基本的には、計算をして、試作をするにたる予測をするのが重要になってくるのである。。
では、どうやって計算をするのか??
一般的な強度計算に対しては、材料力学の教科書を引っ張り出してきて、モデリングしようとしている形状を角柱や円柱に簡易化し、その上で、変形や強さの関係式、安全率の概念を適用すれば、おおよその指針が立つ。その計算で強度がNGならば、CAEをやっても恐らく強度NGで、試作をしても同じである。
例えば、ある部材の変形量に関する議論においては、一つの関係式を元に、結構な設計の見通しを立てることができる。
【最大変形量の関係式】
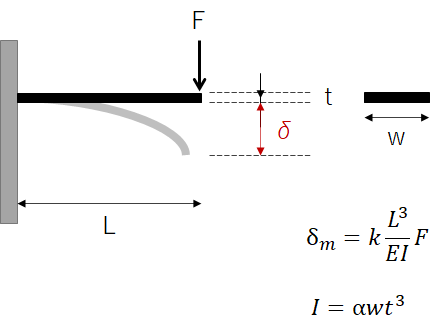
上図は、材料力学の教科書やHPをみれば直ぐにでてくる情報である。
δ:最大変形量、L:材料の長さ、E:縦弾性係数(材料で決まる)、I:断面二次モーメント、F:付加する力、w:材料の幅、t:材料の厚み、kやαは係数。この係数も、前述の教科書やHPを参照すれば、直ぐに出てくる。正の値である。
設計する場において、材料の厚みtを何ミリにすればよいか?という議論があったとする。この時、例えば、上の式において、L,w,E,Fを固定すれば、、、
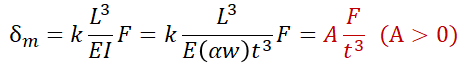
という関係式に整理できる。A=kL^3/(Eαw)
とすれば、、、
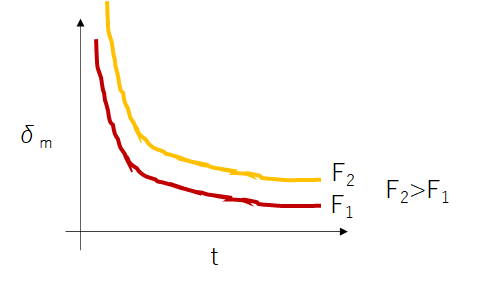
上図のような具合のイメージをすることができる。これによると、ある厚みから先は、変形量が大して変わらなくなるということなので、そのギリギリを攻めよう!という判断が可能になる。因みに、この時は既に使う材料の目星がついているはずである。世の中に出回っている材料には、、特に、板金は、鋼材の厚みがある程度限りがあるので考えやすい。例えば、上の関係式での比較の結果、0.7tと0.8tでは、力に対する変形量は0.1%しか変わらなかったとする。もう一段薄い、0.6tだと、0.7tに対して一気に5%も大きく変形したとする。。。どうやら、今の構造だと、厚みの限界は、0.7tにありそうだ。。。強度、軽さ、流通性を加味して、、よし、07tで行こう!と判断できるのである。
これらは、所詮は、数式の遊びである。
つまり、受験勉強でお馴染みの、「問題を理解して、覚えた知識を当てはめて、その枠組みの中で答えを出す」、、それと同じことである。
よく、社会人になると、、理系の、とりわけエンジニアになると、、学問や数式遊びなんて糞喰らえだ!感覚だ!経験だ!という風潮がある。そういった人たちの設計は、結果的にまともであったとしても、「これは最適なのか?」「それ以外は可能性はないのか?」という問いかけに対して「これが最適ですよ!だって、あれもこうやっているし(=具体例の提示が根拠。その具体例って本当に最適なの?という突っ込みには詰む)」「やってみなきゃわからないです。試作しましょう!(=そんなに予算がないプロジェクトチームはどうすんの?CAEでもやろうかね?)」という具合にしか答えられないのである。
感覚や経験は、もちろん大事である。でも、それが身につくまで若手エンジニアの成長を見守るほど、昨今の開発競争は悠長ではない。また、CAEはデータ作成のためにパソコンの前で四苦八苦することになり、経験豊かな人が使わないと時間がかかってしまう。こんな状況下で、短時間で、見通しのよい設計判断をするためには、数式遊びは極めて有効だと私は思うのである。
後ほど、熱設計に関する数式遊びを紹介したいと思う。。こうした情報発信が、試作前の設計判断の効率化に貢献できれば幸いである。。。では。。
なお、こうした数式の遊びをしたものは、終わった後にフォーマット化しておくと便利です。理由(目的)は下記です。
① 思考の総点検
② 次回以降、一から思考しなくて済む。時間短縮。
③ 入力値をかえたとき、結果の変化を直ぐに見積れる。
フォーマットの作り方は、過去記事を参考下さい。